Թեմա՝ Բազմանկյուն, ուռուցիկ բազմանկյուն
Բազմանկյուն կոչվում է պարզ փակ բեկյալից և նրանով սահմանափակված տիրույթից բաղկացած պատկերը:
Բեկյալի հանգույցները կոչվում են բազմանկյան գագաթներ, իսկ օղերը՝ կողմեր:
Բազմանկյան մի կողմին պատկանող երկու գագաթները կոչվում են հարևան գագաթներ: Երկու ոչ հարևան գագաթները (որոնք չեն գտնվում նույն կողմի վրա) միացնող հատվածը կոչվում է բազմանկյան անկյունագիծ:
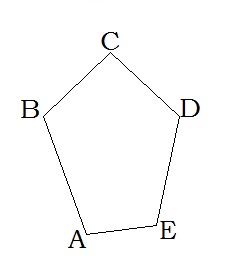
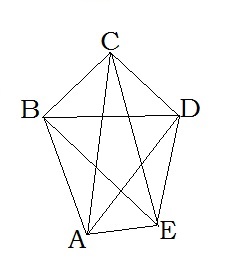
A, B, C, D, E՝ գագաթներ, AB, BC, CD, DE, AE՝ կողմեր, AC, AD, BE, BD, CE՝ անկյունագծեր:
Բոլոր կողմերի երկարությունների գումարը կոչվում է բազմանկյան պարագիծ: Յուրաքանչյուր քազմանկյուն հարթությունը բաժանում է երկու մասի, որոնցից մեկը կոչվում է բազմանկյան ներքին տիրույթ, իսկ երկրորդը՝ արտաքին տիրույթ
Ուռուցիկ n-անկյան անկյունների գումարը:
Ընդհանուր դեպքում, բազմանկյունը կարելի անվանել n-անկյուն, եթե այն ունի n հատ կողմ, n հատ անկյուն և n հատ գագաթ:
Բազմանկյունը կոչվում է ուռուցիկ, եթե այն ընկած է իր ցանկացած երկու հարևան գագաթներով անցնող մի ուղղի կողմում։
Նկարում պատկերված F1 բազմանկյունը ուռուցիկ է, իսկ F2 բազմանկյունը ուռուցիկ չէ:
Ուռուցիկ n-անկյան անկյունների գումարը հավասար է 180°⋅(n−2)-ի:
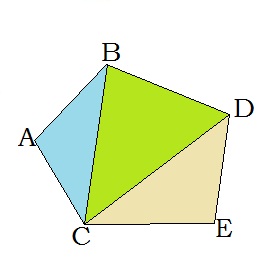
Ցանկացած բազմանկյուն կարելի է բաժանել եռանկյունների: Այդպես է արված վերևի նկարում: Եռանկյունների թիվը 2 -ով քիչ է բազմանկյան կողմերի թվից: Եռանկյունների կողմերը բազմանկյան կողմեր և անկյունագծեր են:
Ցանկացած եռանկյան ներքին անկյունների գումարը 180° է: Հետևաբար, ուռուցիկ n-անկյան անկյունների գումարը 180°⋅(n−2) է:
Հարցեր և առաջադրանքներ։
1. Ո՞ր բազմանկյուն է կոչվում ուռուցիկ։
Բազմանկյունը կոչվում է ուռուցիկ, եթե այն ընկած է իր ցանկացած երկու հարևան գագաթներով անցնող մի ուղղի կողմում։
Եթե ոչ – ապա ուռուցիկ է։
2․ Ի՞նչ բանաձևով են հաշվում բազմանկյան բոլոր անկյունների գումարը։
(n-2)*180°=
3․ Գծագրել ուռուցիկ հնգանկյուն և վեցանկյուն: Բազմանկյուններից յուրաքանչյուրում որևէ գագաթից տարեք բոլոր անկյունագծերը: Տարված անկյունագծերով քանի՞ եռանկյան է տրոհվում բազմանկյուններից յուրաքանչյուրը:
Ըստ կանոնի՝
Բազմանկյունը կոչվում է ուռուցիկ, եթե այն ընկած է իր ցանկացած երկու հարևան գագաթներով անցնող մի ուղղի կողմում։
Դրա համար՝ եթե մեր հնգանկյուն և վեցանկյունը ուռուցիկ է, ապա կարող ենք հաստատ ասել որ տարված անկյունագծերով գծերը չեն տրոհի բազմանկյունները։

4. GEOGEBRA ծրագրով գծիր որևէ բազմանկյուն։շ

Կից անկյուններն են՝ ∠A և ∠D, ∠B և C, ∠A և ∠B, ∠C և D։
Հարևան գագաթներն են՝ A և D, B և C։
ա) Ցույց տուր գագաթները, նշիր կարմիրով
բ) Ցույց տուր կողմերը
գ) Ցույց տուր կից կողմերը
դ) Ցույց տուր հարևան գագաթները։
5.GEOGEBRA ծրագրով գծել ուռուցիկ բազմանկյուն, ինչի՞ է հավասար նրա պարագիծը։

Ես գծեցի հավասարակողմ եռանկյուն, ինչի պատճարով այս դեպքում, իր P-ն հավասար կլինի՝ P=a(կողմեր)*3=
6. GEOGEBRA ծրագրով գծել ոչ ուռուցիկ բազմանկյուն, ցույց տուր որ այն ուռուցիկ չէ։

Բազմանկյունը կոչվում է ուռուցիկ, եթե այն ընկած է իր ցանկացած երկու հարևան գագաթներով անցնող մի ուղղի կողմում։
7. GEOGEBRA ծրագրով գծել ուռուցիկ բազմանկյուն, նշիր նրա արտաքին և ներքին տիրույթները։ Ներքին տիրույթը ներկիր սպիտակ, արտաքին տիրույթը՝ կապույտ։

Հաշվի առնելով ֆոնի գույնը, ներքին անկյունը կապույտ գույնի արեցի։
8.GEOGEBRA ծրագրով գծել եռանկյուն։ Ինչքա՞ն է եռանկյան բոլոր անկյունների աստիճանային գումարը։

Եռանկյան անկյունների գումարը։
Ու կարևոր չի ինչպիսի եռանկյունը է այն, իր անկյունների գումարը միշտ կլինի 180°։
9. GEOGEBRA ծրագրով գծել քառանկյուն։ Ինչքա՞ն է քառանկյան բոլոր անկյունների աստիճանային գումարը։
Ուղղանկյան յուրաքանչյուր անկյուն հավասար է 90°, ինչը նշանակում է՝
90°*4=360°

10. GEOGEBRA ծրագրով գծել հնգանկյուն։ Ինչքա՞ն է հնգանկյան բոլոր անկյունների աստիճանային գումարը։

Այս հարցի պատասխանը կարող ենք պարզել՝ հաշվարկելով, թե քանի եռանկյուն կլինի հնգանկյունից, այնուհետև այդ թիվը բազմապատկելով 180-ով։
(5-2)*180°=540°
11. GEOGEBRA ծրագրով գծել վեցանկյուն։ Ինչքա՞ն է վեցանկյան բոլոր անկյունների աստիճանային գումարը։

Այս հարցի պատասխանը կարող ենք պարզել՝ հաշվարկելով, թե քանի եռանկյուն կլինի հնգանկյունից, այնուհետև այդ թիվը բազմապատկելով 180-ով։
(6-2)*180°=720°
12․ Գտնել ուռուցիկ հնգանկյան անկյունները, եթե դրանք համեմատական են 2, 3, 4, 5, 6 թվերին:
Ինչպես արթեն գիտենք, հնգանկյան անկյունների գումարը 540°։
Ենթադրենք, որ՝ A=2x, B=3x, C=4x, D=5x, E=6x
A+B+C+D+E=540°
2x+3x+4x+5x+6x=540°
540/20=27°
A=27*2=54°
B=27*3=81°
C=27*4=108°
D=27*5=135°
E=27*6=162°
Եկենք ստուգենք՝ 54°+81°+108°+135°+162°=540°
