My hobby is quite unique because I enjoy two different activities: boxing and collecting perfumes. Boxing is a sport that helps me stay fit and focused. I train regularly, improving my strength and endurance. It’s a great way to release stress, and I love the discipline and skill it requires. Sparring with partners and learning new techniques also keeps things exciting. On the other hand, I have a passion for perfumes. I love exploring different fragrances, each one telling its own story through unique blends of ingredients. From floral to woody, fresh to spicy, collecting perfumes gives me an opportunity to appreciate the art of scent creation. In this way, I balance physical activity with my sensory interest in fragrances, making these two hobbies very rewarding.

Թեմա՝ Գործակիցների հավասարեցման (գումարման) կանոնը:

Երկու անհայտներով երկու հավասարումների համակարգի լուծման գումարման (գործակիցների հավասարեցման) եղանակի ալգորիթմը:

1. Հավասարեցնել (եթե անհրաժեշտ է) փոփոխականներից մեկի գործակիցների մոդուլները:
2. Գումարել կամ հանել հավասարումները: Լուծել ստացված մեկ փոփոխականով հավասարումը և գտնել անհայտներից մեկը:  

3. Երկրորդ քայլում գտած արժեքը տեղադրել հավասարումներից որևէ մեկի մեջ և գտնել համակարգի երկրորդ փոփոխականի արժեքը:  

4. Գրել պատասխանը: 

Օրինակ

1. Լուծել հավասարումների համակարգը՝ 

Լուծում:

Գումարենք հավասարումները՝

2. Լուծել հավասարումների համակարգը՝ 

Լուծում: Այս համակարգում փոփոխականների գործակիցները մոդուլով հավասար չեն իրար: Հետևաբար, պետք է հավասարեցնել փոփոխականներից մեկի, օրինակ՝ x-ի գործակիցները: Դրա համար առաջին հավասարումը բազմապատկենք 3-ով, իսկ երկրորդը՝ 5-ով: Հիմա x-ի գործակիցները հավասար են և կարող ենք հավասարումները իրարից հանել: 

Առաջադրանքներ։

1․ Լուծել հավասարումների համակարգը․

2․ Լուծել հավասարումների համակարգը․

3․ Լուծել հավասարումների համակարգը․

Թեմա՝ Սեղան

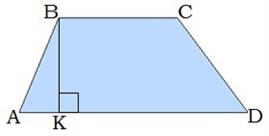
Սեղան է կոչվում այն քառանկյունը, որի երկու կողմերը զուգահեռ են, իսկ մյուս երկուսը զուգահեռ չեն:

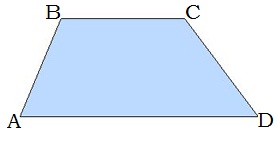
Սեղանի զուգահեռ կողմերը կոչվում են հիմքեր:AD -ն և BC -ն սեղանի հիմքերն են:  

Սեղանի ոչ զուգահեռ կողմերը, կոչվում են սրունքներ: AB -ն և CD -ն սեղանի սրունքներն են:  

Կան սեղանի մի քանի տեսակներ: Հաճախ դիտարկվում են ուղղանկյուն և հավասարասրուն սեղանները:

Ուղղանկյուն սեղան

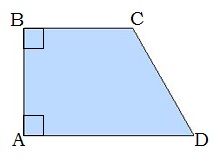
Սեղանը կոչվում է ուղղանկյուն սեղան, եթե նրա սրունքներից որևէ մեկը ուղղահայաց է հիմքերին:

Հավասարասրուն սեղան

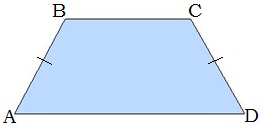
Սեղանը, որի սրունքները հավասար են, կոչվում է հավասարասրուն սեղան:

Սեղանի հատկությունները

Սեղանի ներքին անկյունների գումարը (ցանկացած քառանկյան) 360° է:

Ցանկացած սեղանի սրունքին առընթեր անկյունների գումարը 180° է:

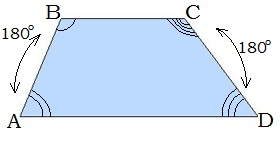
Հավասարասրուն սեղանի հատկությունները

Սեղանը կոչվում է հավասարասրուն, եթե նրա սրունքները հավասար են:

Հետևյալ հատկությունները բնորոշ են միայն հավասարասրուն սեղաններին:

1. Հավասարասրուն սեղանի հիմքերին առընթեր անկյունները զույգ առ զույգ հավասար են:

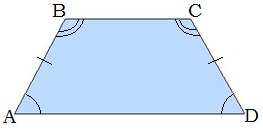
2. Հավասարասրուն սեղանի անկյունագծերը հավասար են:

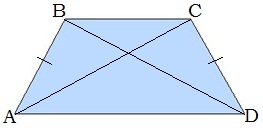
AC=BD

Հավասարասրուն սեղանի հայտանիշները

1. Եթե սեղանի հիմքին առընթեր անկյունները հավասար են, ապա սեղանը հավասարասրուն է:

2. Եթե սեղանի անկյունագծերը հավասար են, ապա սեղանը հավասարասրուն է:

Հարցեր և առաջադրանքներ:

1․ Ո՚ր պատկերն է կոչվում սեղան: GEOGEBRA ծրագրով գծել սեղան:

2․Ինչպե՞ս են կոչվում սեղանի կողմերը:

3․ Ո՚ր պատկերն է կոչվում հավասարասրուն սեղան:

4․ Թվարկել սեղանի տեսակները: GEOGEBRA ծրագրով գծել այդ պատկերները:

5․ Նշել  ճիշտ պնդումը:

ա) Ցանկացած սեղանի հիմքերը զուգահեռ են:

բ) Հավասարասրուն սեղանի սրունքները զուգահեռ են:

գ) Ուղղանկյուն սեղանի հիմքերը հավասար են:

6․ Տրված է՝ ∢A=37°∢C=121°։ Գտնել ∢B,∢D

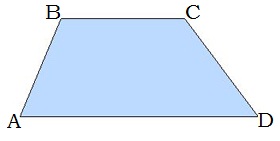
7․ Հաշվել ABCD սեղանի անկյունները, եթե  ∢A=30°

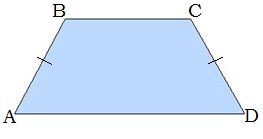
8․ ABCD սեղանի AB սրունքը հիմքի հետ կազմում է 30°: Հաշվիր BK բարձրությունը, եթե AB կողմը 30 սմ է:

9․ Սեղանի հիմքերի հարաբերությունը հավասար է 2:7: Հաշվել սեղանի մեծ հիմքը, եթե նրա փոքր հիմքը հավասար է 12 սմ -ի:

10․ Սեղանի կողմերը հարաբերում են ինչպես՝ 7:6:10:9, իսկ սեղանի պարագիծը 128 սմ է: Հաշվիր սեղանի կողմերը:

Արքիմեդի օրենք

Արքիմեդի օրենքը ձևակերպում է մարմինների լողունակության և հեղուկներում կամ գազերում նրանց վրա ազդող ուժերի հարաբերությունը:

Ըստ Արքիմեդի օրենքի՝ մարմնի վրա հեղուկում (կամ գազում) ընկղմվելու դեպքում ազդում է վեր բարձրացող ուժ, որը հավասար է մարմնի կողմից տեղահանված հեղուկի (կամ գազի) քաշին: Այս ուժը կոչվում է լողացման ուժ կամ Արքիմեդյան ուժ:

Օրենքը կարելի է ձևակերպել հետևյալ կերպ.
«Յուրաքանչյուր մարմին, որը ամբողջությամբ կամ մասնակիորեն ընկղմված է հեղուկի մեջ, իր վրա զգում է վեր ուղղված լողացման ուժ, որը հավասար է տեղահանված հեղուկի ծանրությանը»:

Արքիմեդի օրենքը կիրառվում է տարբեր ոլորտներում, ինչպիսիք են նավաշինությունը, օդագնացությունը, սուզանավերի նախագծումը և այլն:

Արքիմեդի Ուժ

Արքիմեդի ուժը (կամ լողացման ուժ) այն վեր ուղղված ուժն է, որը ազդում է մարմնի վրա, երբ այն ամբողջությամբ կամ մասնակիորեն ընկղմված է հեղուկի կամ գազի մեջ: Այս ուժը առաջանում է հեղուկի կամ գազի ճնշման տարբերությունից, որը գործում է մարմնի տարբեր մասերի վրա:

F Արքիմեդ​ — Արքիմեդի ուժը,

ρ — հեղուկի (կամ գազի) խտությունը,

v — մարմնի տեղահանած հեղուկի (կամ գազի) ծավալը,

g — ծանրության արագացումն է (մոտավորապես 9.8, {մ/վ^2} երկրի մակերևույթին):

Այս ուժը էական նշանակություն ունի լողացող մարմինների համար. եթե Արքիմեդի ուժը մեծ է մարմնի քաշից, մարմինը կլողա, իսկ եթե փոքր է, ապա կխորտակվի: