1․ Ի՞նչ է սինուսը, կոսինուսը և տանգենսը:

Ուղղանկյուն եռանկյան սուր անկյան սինուս կոչվում է այդ անկյան դիմացի էջի հարաբերությունը ներքնաձիգին:

Ուղղանկյուն եռանկյան սուր անկյան կոսինուս կոչվում է այդ անկյան կից էջի հարաբերությունը ներքնաձիգին:

Ուղղանկյուն եռանկյան սուր անկյան տանգենս կոչվում է այդ անկյան դիմացի էջի հարաբերությունը կից էջին:

2․ ABC ուղղանկյուն եռանկյան սուր անկյունների սինուսի, կոսինուսի և տանգենսի արժեքների վերաբերյալ ո՞ր բանաձևերն են ճիշտ:

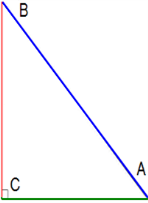
ա) tgA=CB/CA բ)tgA=CA/CB գ) բոլորն էլ սխալ են դ) cosA=AC/AB

ե) sinB=AC/AB զ) բոլորն էլ ճիշտ են է) sinB=AB/CB ը) cosA=AC/AB

3․ Գտնել D անկյան սինուսը, կոսինուսը և տանգենսը;

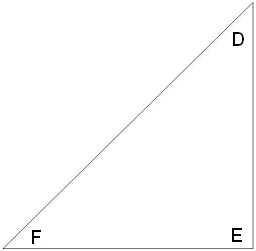
sinD=FE/FD

conD=DE/DF

tgD=EF/ED

4․ Գտնել F անկյան սինուսը,կոսինուսը և տանգենսը:

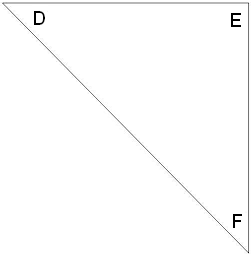
sinF=ED/DF

conF=EF/DF

tgF=ED/EF

5․ Տրված է ABC ուղղանկյուն եռանկյունը: Գտնել A անկյան սինուսն ու կոսինուսը: 

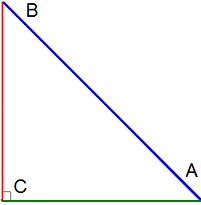
ա) Ո՞րն է A անկյան սինուսը՝    BC/BA CB/AC CA/BA

բ) Ո՞րն է A անկյան կոսինուսը՝ CA/BA CB/AC BC/BA

6․ Կամայական ուղղանկյուն եռանկյան սուր անկյան սինուսը փոքր է մեկից: Բացատրել, ինչո՞ւ

Սինուսը փոքր է մեկից որովհետև դիմացի էջը միշտ փոքր է ներքնաձիգից և երբ որ փոքր թիվը բաժանում ենք մեծ թվի միշտ մեկից փոքր է լինում պատասխանը։

7․ Կարո՞ղ է մեկից մեծ արժեք ունենալ ուղղանկյուն եռանկյան սուր անկյան ա) կոսինուսը բ) տանգենսը: Պատասխանը հիմնավորել:

Կոնսինուսը չի կարող որովհետև կից կողմը փոքր է ներքնաձիգից և փոքր թիվ բաժանաց մեծ թվի հավասար է լինում եկից փոքր։ Տանգենսը կարող է մեկից մեծ լինել որովհետև 2 էջերը կարող են հավասար լինել մեծ լինել կամ փոքր լինել իրարից։

8. Գծել ABC ուղղանկյուն եռանկյունը այնպես, որ ∠C=90°, CA=6 սմ և CB=10 սմ: Գտնել A և B սուր անկյունների սինուսը, կոսինոիսը և տանգենսը:

AC²+CB²=AB^2. 6²+10²=AB^2. 36+100=AB^2. AB²=136. AB=√136.

sinA=10/√136=0.859. cosA=6/√136=0.515. tgA=10/6=1.667

sinB=6/√136=0.515. cosB=10/√136=0.859. tgB=6/10=0.6

9. ABC ուղղանկյուն եռանկյան մեջ C -ն ուղիղ անկյունն է, CA=18 սմ և CB=24 սմ: Հաշվել B անկյան տանգենսը, սինուսը և կոսինուսը:

AC²+CB²=AB^2. 18²+24²=AB^2. 324+576=AB^2. AB²=900. AB=√900. AB=30

sinB=18/30=0.6. conB=24/30=0.8. tgB=18/24=0.75

Գիտելիքների ստուգում

1․ Զուգահեռագծի մակերեսը։

S = a × h a-ն կողմն է, իսկ h-ը՝ այդ կողմին տարված բարձրությունը:

2․ Գտնել քառակուսու մակերեսը, եթե նրա կողմը   հավասար է  5 դմ։

S = a² = 5² = 25 դմ²

3․ Գտնել ուղղանկյան անհայտ կողմը, եթե նրա  մակերեսը 24 սմ², իսկ կողմերից մեկը 4 սմ է։

S = a × b ⇒ 24 = 4 × b ⇒ b = 24 / 4 = 6 սմ

4․Հաշվել շեղանկյան մակերեսը, եթե նրա  կողմը 20 դմ է, իսկ այդ կողմին տարված    բարձրությունը 17 դմ է:

S = a × h = 20 × 17 = 340 դմ²

5․ Գտնել ուղղանկյուն եռանկյան մակերեսը, եթե    նրա էջերն են 4 սմ և 12 սմ։

S = (a × b) / 2 = (4 × 12) / 2 = 48 / 2 = 24 սմ²

6․ Գտնել AD և BC հիմքերով ABCD սեղանի  մակերեսը, եթե CD⊥AD, AD=13 սմ, CD=8 սմ, BC=5 սմ:

S = ((a + b) × h) / 2,

a = AD = 13 սմ, b = BC = 5 սմ, h = CD = 8 սմ

S = ((13 + 5) × 8) / 2 = (18 × 8) / 2 = 144 / 2 = 72 սմ²