My hobby is quite unique because I enjoy two different activities: boxing and collecting perfumes. Boxing is a sport that helps me stay fit and focused. I train regularly, improving my strength and endurance. It’s a great way to release stress, and I love the discipline and skill it requires. Sparring with partners and learning new techniques also keeps things exciting. On the other hand, I have a passion for perfumes. I love exploring different fragrances, each one telling its own story through unique blends of ingredients. From floral to woody, fresh to spicy, collecting perfumes gives me an opportunity to appreciate the art of scent creation. In this way, I balance physical activity with my sensory interest in fragrances, making these two hobbies very rewarding.

Թեմա՝ Գործակիցների հավասարեցման (գումարման) կանոնը:

Երկու անհայտներով երկու հավասարումների համակարգի լուծման գումարման (գործակիցների հավասարեցման) եղանակի ալգորիթմը:

1. Հավասարեցնել (եթե անհրաժեշտ է) փոփոխականներից մեկի գործակիցների մոդուլները:
2. Գումարել կամ հանել հավասարումները: Լուծել ստացված մեկ փոփոխականով հավասարումը և գտնել անհայտներից մեկը:  

3. Երկրորդ քայլում գտած արժեքը տեղադրել հավասարումներից որևէ մեկի մեջ և գտնել համակարգի երկրորդ փոփոխականի արժեքը:  

4. Գրել պատասխանը: 

Օրինակ

1. Լուծել հավասարումների համակարգը՝ 

Լուծում:

Գումարենք հավասարումները՝

2. Լուծել հավասարումների համակարգը՝ 

Լուծում: Այս համակարգում փոփոխականների գործակիցները մոդուլով հավասար չեն իրար: Հետևաբար, պետք է հավասարեցնել փոփոխականներից մեկի, օրինակ՝ x-ի գործակիցները: Դրա համար առաջին հավասարումը բազմապատկենք 3-ով, իսկ երկրորդը՝ 5-ով: Հիմա x-ի գործակիցները հավասար են և կարող ենք հավասարումները իրարից հանել: 

Առաջադրանքներ։

1․ Լուծել հավասարումների համակարգը․

2․ Լուծել հավասարումների համակարգը․

3․ Լուծել հավասարումների համակարգը․

Թեմա՝ Սեղան

Սեղան է կոչվում այն քառանկյունը, որի երկու կողմերը զուգահեռ են, իսկ մյուս երկուսը զուգահեռ չեն:

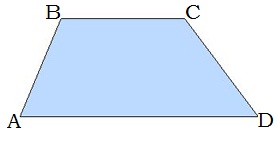
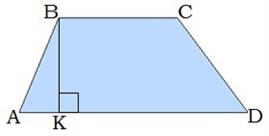
Սեղանի զուգահեռ կողմերը կոչվում են հիմքեր:AD -ն և BC -ն սեղանի հիմքերն են:  

Սեղանի ոչ զուգահեռ կողմերը, կոչվում են սրունքներ: AB -ն և CD -ն սեղանի սրունքներն են:  

Կան սեղանի մի քանի տեսակներ: Հաճախ դիտարկվում են ուղղանկյուն և հավասարասրուն սեղանները:

Ուղղանկյուն սեղան

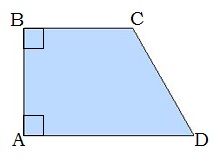
Սեղանը կոչվում է ուղղանկյուն սեղան, եթե նրա սրունքներից որևէ մեկը ուղղահայաց է հիմքերին:

Հավասարասրուն սեղան

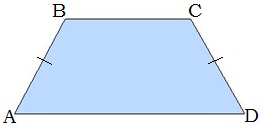
Սեղանը, որի սրունքները հավասար են, կոչվում է հավասարասրուն սեղան:

Սեղանի հատկությունները

Սեղանի ներքին անկյունների գումարը (ցանկացած քառանկյան) 360° է:

Ցանկացած սեղանի սրունքին առընթեր անկյունների գումարը 180° է:

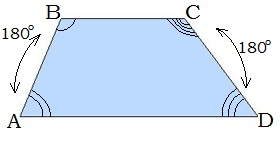
Հավասարասրուն սեղանի հատկությունները

Սեղանը կոչվում է հավասարասրուն, եթե նրա սրունքները հավասար են:

Հետևյալ հատկությունները բնորոշ են միայն հավասարասրուն սեղաններին:

1. Հավասարասրուն սեղանի հիմքերին առընթեր անկյունները զույգ առ զույգ հավասար են:

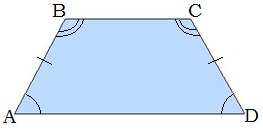
2. Հավասարասրուն սեղանի անկյունագծերը հավասար են:

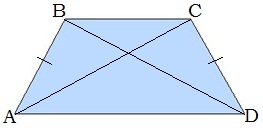
AC=BD

Հավասարասրուն սեղանի հայտանիշները

1. Եթե սեղանի հիմքին առընթեր անկյունները հավասար են, ապա սեղանը հավասարասրուն է:

2. Եթե սեղանի անկյունագծերը հավասար են, ապա սեղանը հավասարասրուն է:

Հարցեր և առաջադրանքներ:

1․ Ո՚ր պատկերն է կոչվում սեղան: GEOGEBRA ծրագրով գծել սեղան:

2․Ինչպե՞ս են կոչվում սեղանի կողմերը:

3․ Ո՚ր պատկերն է կոչվում հավասարասրուն սեղան:

4․ Թվարկել սեղանի տեսակները: GEOGEBRA ծրագրով գծել այդ պատկերները:

5․ Նշել  ճիշտ պնդումը:

ա) Ցանկացած սեղանի հիմքերը զուգահեռ են:

բ) Հավասարասրուն սեղանի սրունքները զուգահեռ են:

գ) Ուղղանկյուն սեղանի հիմքերը հավասար են:

6․ Տրված է՝ ∢A=37°∢C=121°։ Գտնել ∢B,∢D

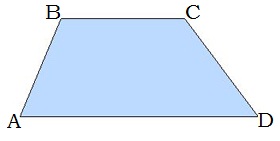
7․ Հաշվել ABCD սեղանի անկյունները, եթե  ∢A=30°

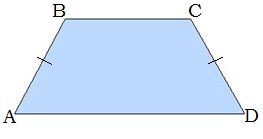
8․ ABCD սեղանի AB սրունքը հիմքի հետ կազմում է 30°: Հաշվիր BK բարձրությունը, եթե AB կողմը 30 սմ է:

9․ Սեղանի հիմքերի հարաբերությունը հավասար է 2:7: Հաշվել սեղանի մեծ հիմքը, եթե նրա փոքր հիմքը հավասար է 12 սմ -ի:

10․ Սեղանի կողմերը հարաբերում են ինչպես՝ 7:6:10:9, իսկ սեղանի պարագիծը 128 սմ է: Հաշվիր սեղանի կողմերը:

Արքիմեդի օրենք

Արքիմեդի օրենքը ձևակերպում է մարմինների լողունակության և հեղուկներում կամ գազերում նրանց վրա ազդող ուժերի հարաբերությունը:

Ըստ Արքիմեդի օրենքի՝ մարմնի վրա հեղուկում (կամ գազում) ընկղմվելու դեպքում ազդում է վեր բարձրացող ուժ, որը հավասար է մարմնի կողմից տեղահանված հեղուկի (կամ գազի) քաշին: Այս ուժը կոչվում է լողացման ուժ կամ Արքիմեդյան ուժ:

Օրենքը կարելի է ձևակերպել հետևյալ կերպ.
«Յուրաքանչյուր մարմին, որը ամբողջությամբ կամ մասնակիորեն ընկղմված է հեղուկի մեջ, իր վրա զգում է վեր ուղղված լողացման ուժ, որը հավասար է տեղահանված հեղուկի ծանրությանը»:

Արքիմեդի օրենքը կիրառվում է տարբեր ոլորտներում, ինչպիսիք են նավաշինությունը, օդագնացությունը, սուզանավերի նախագծումը և այլն:

Արքիմեդի Ուժ

Արքիմեդի ուժը (կամ լողացման ուժ) այն վեր ուղղված ուժն է, որը ազդում է մարմնի վրա, երբ այն ամբողջությամբ կամ մասնակիորեն ընկղմված է հեղուկի կամ գազի մեջ: Այս ուժը առաջանում է հեղուկի կամ գազի ճնշման տարբերությունից, որը գործում է մարմնի տարբեր մասերի վրա:

F Արքիմեդ​ — Արքիմեդի ուժը,

ρ — հեղուկի (կամ գազի) խտությունը,

v — մարմնի տեղահանած հեղուկի (կամ գազի) ծավալը,

g — ծանրության արագացումն է (մոտավորապես 9.8, {մ/վ^2} երկրի մակերևույթին):

Այս ուժը էական նշանակություն ունի լողացող մարմինների համար. եթե Արքիմեդի ուժը մեծ է մարմնի քաշից, մարմինը կլողա, իսկ եթե փոքր է, ապա կխորտակվի:

Դասի հղում։

Այլ հղումներ՝ 1,  2

1. Բնութագրել Ֆրանսիայի աշխարհագրական դիրքը: 
2. Որո՞նք են ֆրանսիայի տնտեսության զարգացման նախադրյալները
3. Ի՞նչ դեր ունի Ֆրանսիան ժամանակակից աշխարհում և տարածաշրջանում:
4. Որոնք են Ֆրանսիայիում զբոսաշրջության և հանգստի կազմակերպման ռեսուրսները։

• Բնութագրել Ֆրանսիայի աշխարհագրական դիրքը: 

Ֆրանսիան գտնվում է Եվրոպայի ծայր արևմուտքում և ունի շատ հարմար տնտեսաաշխարհագրական դիրք։ Աշխարհագրական դիրքի բնորորշ գծերն են ա) հարմար հարևանային դիրքը։ Նրա բոլոր հարևանները Եվրամիության անդամ զարգացած երկրներ են։ բ) Երկու անգամ ավելի երկար ծովային սահմանները, քան ցամաքայինը։ Ատլանտյան օվկիանոսի և նրա մասը կազմող Միջերկրական ծովի հետ սահմանակցումը հնարավորություն է տալիս ակտիվ մասնակցություն ունենալ համաշխարհային ծովային առևտրին։ գ) Տարանցիկ դիրքը, քանի այստեցով են անցնում Մեջորկրական ծովից դեպի Հյուսիսային ծով և Իսպանիայից դեպի Իտալիա ու Եվրոպայի այլ երկրներ անցնող կարևոր ճանապարհները։

• Որո՞նք են ֆրանսիայի տնտեսության զարգացման նախադրյալները

Հարմար աշխարհագրական դիրքը, համեմատաբար հարթ մակերևույթը, բնական պաշարները, հարուստ ջրային և հողային ռեսուրսներ, բարենպաստ կլիմա։

• Ի՞նչ դեր ունի Ֆրանսիան ժամանակակից աշխարհում և տարածաշրջանում:

Ֆրանսիան Եվրամիության և Եվրոպական խորհդրի հիմնադիրներից է։ Ֆրանսիական Ստրասբուրգ քաղաքում գտնվում են Եվրախորհրդարանը և Եվրոպական խորհրդը։ Ֆրանսիան բնապահպանության համար պայքարող առաջատար երկրներից է, ինչպես նաև մարդու իրավունքների, ժողովրդավարության համար պայքարող։ Ֆրանսիայի հայտնի կարգախոսն է՝ ազատություն, հավասարություն, եղբայրություն։

• Որոնք են Ֆրանսիայիում զբոսաշրջության և հանգստի կազմակերպման ռեսուրսները։

Միջերկրական ծովի բարձրորակ լողափերը, Ալպերի հանգստավայրերը, զարգացած ճանապարհային և տրանսպորտային ցանցը, պատմամշակութային վայրերը, ճարտարապետություն։ Տարեկան ֆրանսիան այցելում են 70-75 միլիոն զբոսարջիկ։

1․Ի՞նչն են անվանում մեխանիկական շարժում։

Մեխանիկական շարժումը ժամանակի ընթացքում մարմնի դիրքի փոփոխությունն է ուրիշ մարմինների նկատմամբ:

2.Բերել մեխանիկական շարժման օրինակներ։

Մեխանիկական շարժման օրինակներ են՝ գնդակի գլորվելը, մեքենայի գնալը, մարդու քայլելը և այլն:

3.Ո՞ր մարմինն են անվանում հաշվարկման մարմին

Հաշվարկման մարմինը այն մարմինն է, որի նկատմամբ դիտարկվում է ուրիշ մարմինների շարժումը:

4.Ի՞նչն են անվանում նյութական կետ։

Նյութական կետը այն մարմինն է, որի չափերը տվյալ պայմաններում կարելի է անտեսել:

5.Ո՞ր դեպքում մարմինը կարելի է համարել նյութական կետ,ո՞ր դեպքում՝ոչ։

Եթե մարմնի չափերը տվյալ պայմաններում կարելի է անտեսել, այդ կետը կարելի է համարել նյութական կետ: Իսկ եթե տվյալ պայմաններում չի կարելի է անտեսել մարմնի չափերը, այն չի համարվում նյութական կետ:

6.Ի՞նչն են անվանում շարժման հետագիծ։

Հետագիծը այն գիծն է, որով տվյալ հաշվարկման համակարգում շարժվում է մարմինը:

7.Ինչն են անվանում մարմնի անցած ճանապարհ։

Advertisement

Մարմնի անցած ճանապարհը հետագծի այն տեղամասն է, որով շարժվել է մարմինը որոշակի ժամանակամիջոցում:

8.Ինչո՞վ է տարբերվում հետագիծն անցած ճանապարհից:

Հետագիծը տարբերվում է անցած ճանապարհից նրանով, որ անցած ճանապարհը որոշակի ժամանակամիջոցում է ընթանում իսկ հետագիծը կարևոր չէ ինչ ժամանակամիջոցում է ընթանում:

9.Ո՞ր շարժումն է կոչվում հավասաաչափ,ո՞րը անհավասարաչափ։

Այն շարժումը, որի ընթացքում մարմինը կամայական հավասար ժամանակամիջոցներում անցնում է հավասար ճանապարհներ, կոչվում է հավասարաչափ շարժում:

Անհավասարաչափ շարժումները այն են, երբ հավասար ժամանակամիջոցներում մարմինն անցնում է անհավասար ճանապարհներ։

10.Ո՞ր մեծությունն է կոչվում հավասարաչափ շարժման արագություն ՝գրել բանաձևը

Հավասարաչափ շարժման արագությունը ֆիզիկական մեծություն է, որը հավասար է մարմնի անցած ճանապարհի հարաբերությանն այն ճամանակամիջոցին, որի ընթացքում մարմինն անցել է այդ ճանապարհը:

11․Ի՞նչ միավորներով է չափվում արագությունը՝ՄՀ-ում

ՄՀ֊ում որպես արագության միավոր ընդունված է այն հավասարաչափ շարժման արագությունը, որի դեպքում մարմինը 1վ֊ում անցնում է 1մ ճանապարհ։ Այդ միավորը նշանակում են 1 մ/վ։

12․Ինչպե՞ս որոշել հավասարաչափ շարժվող մարմնի անցած ճանապարհը,եթե հայտնի է նրա արագությունը ու շարժման ժամանակը,գրել բանաձևը

Հավասարաչափ շարժման դեպքում մարմնի անցած ճանապարհը որոշելու համար նրա արագությունը պետք է բազմապատկել շարժման ժամանակով։

s=v×t

13.Ինչպե՞ս որոշել հավասարաչափ շարժման ժամանակը,եթե հայտնի են մարմնի արագությունն ու ճանապարհը,գրել բանաձևը:

Հավասարաչափ շարժման ժամանակը որոշելու համար պետք է մարմնի անցած ճանապարհը բաժանել նրա արագությանը։

t=s/v

14․Մեխանիկայի ո՞ր բաժինն  են անվանում կինեմատիկա։Ի՞նչ է ուսումնասիրում մեխանիկայի  <<դինամիկա>> բաժինը

Այն բաժինը որը ուսումնասիրում մարմինների շարժումը առանց պատճառների քննարկման կոչվում է կինեմատիկա։

15․Սահմանել աանհավասարաչափ շարժման միջին  արագություն։

Միջին արագությունը այն ֆիզիկական մեծությունն է, որը հավասար է մարմնի անցած ճանապարհի և այդ ճանապարհն անցնելու ժամանակի հարաբերությանը։

16․Գրել միջին արագության բանաձևը։

Միջին արագության բանաձևն է․
Vմիջ = S/t
Vմիջ – միջին արագություն
S – ճանապարհ
t – ժամանակ

Задания 1. Прочитайте текст и дайте ответы на вопросы:

Этим летом мне довелось ехать в поезде вместе с мальчиком лет двенадцати и его мамой. Он сидел, уткнувшись в книгу, и увлечённо читал «Тараса Бульбу» Гоголя. – Мой сын прямо-таки глотает книги, – сказала женщина. – В отличие от многих его сверстников, он очень начитанный.

Я поинтересовалась, книги каких авторов он читал, и паренёк вытащил из рюкзака блокнот с длинным списком произведений русских и зарубежных классиков и современных писателей. Я обрадовалась: значит, и среди современных подростков встречаются книгочеи! – Мы в классе соревнуемся, кто за лето больше книг прочтёт, – сообщил он. – Я в прошлом году был первым.

У меня на коленях лежал томик Льва Николаевича Толстого, раскрытый на страницах повести «Хаджи-Мурат», и я углубилась в чтение. – А вы за сколько минут страницу прочитываете? – вдруг услышала я голос паренька. – Не заметила… не считала! – А я заметил: пока вы пятнадцать страниц прочитали, я уже двадцать три успел! – Да зачем ты торопишься? Не торопись, вдумывайся в то, что читаешь, иначе пропустишь что-нибудь важное. – Важное-то я не пропущу, – ответил он самоуверенно. – Я только описания природы пропускаю, всякие там облака, цветочки-лепесточки.

Поезд уже подходил к станции, а мне так хотелось поговорить с юным попутчиком. «А ведь читать-то ты, дружок, не умеешь, – хотела я сказать ему. – Из книги берёшь самую малость, только цепочку событий. А книга готова дать тебе бесценный клад мыслей и чувств, научит тебя читать не только строки, но и между строк…» И пока мне думалось, что этих слов он вовсе не поймёт, пока я сердилась сама на себя, решая, как бы мне растревожить этого самоуверенного мальчишку, поезд стал замедлять ход.

Мать мальчика, обращаясь ко мне, восхищённо сказала: – Вы только взгляните! Он уже проглотил книгу! И тут я, наверное, обидела её. – Вы заблуждаетесь, – ответила я. – Он вовсе не умеет читать.

Вопросы:

1.Что сказала его мама о его увлечении чтением?

Мама сказала мальчику, что он очень увлечен чтением и “проглатывает” книги, в отличие от многих его сверстников, он очень начитанный.

2.Что хочет сказать рассказчица мальчику о чтении и восприятии книг?

Он не умеет читать по-настоящему, поскольку он быстро читает, пропуская важные детали, как такие описания природы, и берет из книг только события, а не более глубокие смыслы и эмоции. Она считает, что нужно не торопиться.

3.Какие темы и чувства, по мнению рассказчицы, можно извлечь из книг?

Из книг можно вывести глубокие мысли, чувства, жизненные уроки и скрытые смыслы, которые помогают понять мир и людей.

Задание 2. Вставьте пропущенные буквы и подберите проверочные слова.

1.В_зить – Возить

2.Почин_ть – Починить

3.Бр_дить – Бродить

4.Х_дить – Ходить

5.Х_лмы – Холмы

6.Ст_лбы – Столбы

7.В_сы – Весы

8.Д_ма – Дома

Задание 3. Напиши словами цифры.

1527, 2500, 1933, 2024, 1812

1527 — тысяча пятьсот двадцать семь
2500 — две тысячи пятьсот
1933 — тысяча девятьсот тридцать три
2024 — две тысячи двадцать четыре
1812 — тысяча восемьсот двенадцать

Задание 4. Напишите альтернативный конец истории, в котором мальчик по-другому реагирует на замечания рассказчицы о чтении. Как это меняет их взаимодействие?

В альтернативном конце мальчик, услышав замечания рассказчицы о чтении, заинтересовывается и начинает задавать вопросы. Он делится своими впечатлениями от книг, и рассказчица с радостью предлагает новые рекомендации. Их взаимодействие становится теплым и доверительным, а мальчик начинает воспринимать чтение как увлекательное занятие.

1. Նշել Գերմանիայի աշխարհագրական դիրքի առավելություններն ու թերությունները: Գերմանիան գտնվում է արևմտյան Եվրոպայում, ունի ծով ունի նավթ, իսկ թերություն չունի։ Նաև ունի շատ լավ աշխարհագրական դիրք։
2. Նշել Գերմանիայի տնտեսության զարգացման նախադրյալները: Գործին նվիրվածություն աշխատասիրություն։
3. Ի՞նչ դեր ունի Գերմանիան ժամանակակից աշխարհում: Գերմանիան ունի բազում արտադրություններ, օրինակ՝ ավտոմեքենաներ, վերելակներ և այլն։
4. Ուրվագծային քարտեզի վրա նշել Գերմանիայի հարևան պետությունները, ափերը ողողող ջրային ավազանները:
5. Գերմանիան քանի՞ երկրամաս ունի: 16 երկրամաս։
6. Թվարկի՛ր խոշոր գետերը: Ռեյն, Դանուբ, Էլբա, Վեզեր, Մայն։
7. Բնակչության մասին ի՞նչ գիտես: Նրանց բնակչությունը կազմում է 84 միլիոն մար

Դասի հղում։

Быть современным подростком сложно из-за нескольких факторов:

Социальные сети создают давление из-за постоянных сравнений и кибербуллинга.

Образование требует успеха, вызывая стресс и тревожность.

Психическое здоровье часто страдает из-за высоких ожиданий и неопределенности будущего.

Социальные изменения (экология, политика) усиливают тревогу.

Поиск себя в условиях множества возможностей может запутать.

С другой стороны, технологии и открытость дают подросткам новые возможности для развития и самовыражения.

Թեմա՝ Եռանկյան միջին գիծը։

Եռանկյան երկու կողմերի միջնակետերը միացնող հատվածը կոչվում է այդ եռանկյան միջին գիծ:

Միջին գծի հատկությունը

Եռանկյան միջին գիծը զուգահեռ է եռանկյան կողմերից մեկին և հավասար է այդ կողմի կեսին:

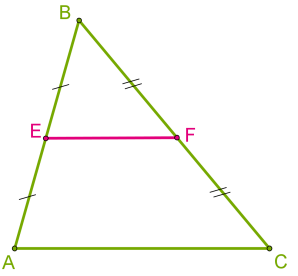
DE∥BC DE=BC/2

Յուրաքանչյուր եռանկյուն ունի երեք միջին գիծ:

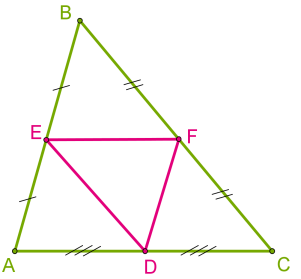
Միջին գծերն են DE, EF և DF հատվածները:

Թալեսի* թեորեմը

Եթե անկյան կողմերը հատող զուգահեռ ուղիղները անկյան մի կողմի վրա անջատում են հավասար հատվածներ, ապա նրանք անկյան մյուս կողմի վրա ևս անջատում են հավասար հատվածներ:

Թալեսի թեորեմը օգտագործում են տրված հատվածը մի քանի հավասար մասերի բաժանելու համար:

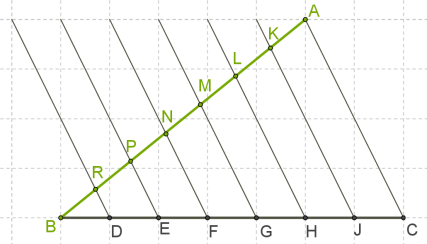
Պետք է AB հատվածը բաժանել 7 հավասար մասերի:  

Գծենք անկյուն, որի մի կողմի վրա ընկած է AB հատվածը: BC կողմը գծենք վանդակների միջոցով՝ հորիզոնական ուղղությամբ: Վանդակները օգտագործում ենք կողմը 7 հավասար մասերի բաժանելու համար՝ BD=DE=EF=FG=GH=HJ=JC:

Երկու հատվածների ծայրակետերը միացնում ենք և ստանում AC հատվածը: J,H,G,F,E,D կետերից տանենք AC -ին զուգահեռ 7 ուղիղներ (նորից օգտագործում ենք վանդակները):

Եթե BD=DE=EF=FG=GH=HJ=JC և AC∥JK∥HL∥GM∥FN∥EP∥DR, ապա, ըստ Թալեսի թեորեմի՝ BR=RP=PN=NM=ML=LK=KA:

*Թեորեմը կոչվում է հին հույն գիտնական Թալես Միլեթացու (մ.թ.ա. մոտ 625-547 թթ.) անունով:

Առաջադրանքներ։

1․ Գրել եռանկյան միջին գծի սահմանումը։ Միջին գիծը դա եռանկյան կողմերից երկուսի մեջտեղում գտնվող միացնող գիծն է։

2․ Գրել միջին գծի հատկությունը։ Եռանկյան միջին գիծը զուգահեռ է եռանկյան կողմերից մեկին և հավասար է այդ կողմի կեսին:

3․ RS -ը  ABC եռանկյան միջին գիծն է՝ R∈AB, S∈AC։ Ընտրել  ճիշտ տարբերակը:

ա) RS∥BC բ) RS⊥AB գ) երկուսն էլ ճիշտ են

4․ LMN եռանկյան մեջ GH-ը միջին գիծ է՝  G∈LM, H∈LN: Միջին գծի  վերաբերյալ, ո՞ր պնդումն է ճիշտ: Ընտրել  ճիշտ պատասխան:

ա) GH=2MN բ) GH=MN/2 գ) երկուսն էլ ճիշտ են

5. BA և FE հատվածների հարաբերությունը հավասար է XY և ML հատվածների հարաբերությանը: BA= 2 դմ, FE= 8 դմ և ML=72 դմ: Հաշվել  XY հատվածի երկարությունը:

BA:FE=XY:ML

2:8=XY:72

XY=72*2:8=18 դմ

6․ ABC եռանկյան AC կողմի երկարությունը 26 սմ է: Հաշվել EF միջին գծի երկարությունը:

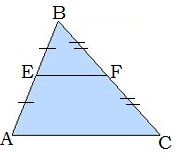
AC = 26 սմ

EF = ?

26/2 = 13 սմ

EF = 13 սմ

7․ Հաշվել AB կողմի երկարությունը, եթե ABC եռանկյան մեջ BC=CD և AE=ED, իսկ CE=8 սմ է։

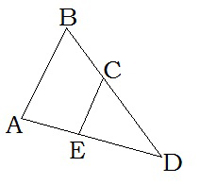
CE = 8 սմ

AB = ?

8 * 2 = 16 սմ

AB = 16 սմ

8․ Քառակուսու անկյունագծի երկարությունը 20 սմ է: Հաշվել այն քառակուսու պարագիծը, որի գագաթները գտնվում են տրված քառակուսու միջնակետերում:

AC = 20 սմ

FE = AH : 2 = 20 : 2 : 2 = 5 սմ

GE = HD : 2 = 20 : 2 : 2 = 5 սմ

P = 5 * 4 = 20 սմ

9․ Տրված է CD=7 մմ հատվածը և հատվածների հարաբերությունը՝ CD/LK=10/6։ Հաշվել LK հատվածի երկարությունը: CD : LD = 10 : 6

LD = 7 * 6 / 10 = 4,2 մմ

10․ Եռանկյան կողմերը հավասար են 8 սմ, 10 սմ, 12 սմ: Գտնել այն եռանկյան պարագիծը, որի կողմերը տրված եռանկյան միջին գծեր են: GEOGEBRA ծրագրով գծել գծագիրը։

P = ?

8/2 = 4 սմ

10/2 = 5սմ

12/2 = 6սմ

P = 4 + 5 + 6 = 15սմ

P = 15սմ

11․ Ուռուցիկ քառանկյան անկյունագծերը հավասար են 14 մ և 20 մ: Գտնել այն քառանկյան կողմերը, որի գագաթները տրված քառանկյան կողմերի միջնակետերն են: GEOGEBRA ծրագրով գծել գծագիրը։

BC = 20 սմ

AD = 14 սմ

EH = BC/2 = 20/2 = 10 սմ

HF = AD/2 = 14/2 = 7 սմ

EH = GF = 10 սմ

HF = EG = 7 սմ