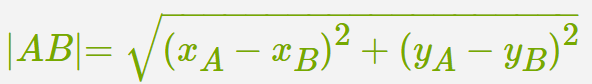
Թեմա՝ Շրջանագծի հավասարումը։

Դուրս բերենք տրված կենտրոնով և տրված շառավղով շրջանագծի հավասարումը:

1. Շրջանագծի բոլոր կետերը գտնվում են միևնույն կետից (կենտրոն) միևնույն հեռավորության վրա (շառավիղ):

2. Մենք ունենք երկու կետերի միջև հեռավորության հաշվման բանաձևը՝ 

Բարձրացնելով քառակուսի, ստանում ենք՝

Դիցուք շրջանագծի կենտրոնը C(x_C;y_C) կետն է, իսկ շառավիղը՝ R-ն է: 

Շրջանագծի ցանկացած P(x;y) կետ գտնվում է C կենտրոնից R հեռավորության վրա:

Հետևաբար, տեղի ունի հետևյալ հավասարությունը՝ 

(x−x_O)²+(y−y_O)²=R²

Սա հենց C կենտրոնով և R շառավղով շրջանագծի հավասարումն է:

Եթե շրջանագծի կենտրոնը կոորդինատների (0;0) սկզբնակետն է, ապա հավասարումը ստանում է հետևյալ տեսքը՝ x²+y²=R² ։

Առաջադրանքներ․

1․ A(2; 3), B(3; 4), C(5; 0), D(-4; 5), E(-3; 4) կետերից որո՞նք են գտնվում x²+ y² = 25 հավասարմամբ որոշվող շրջանագծի վրա:

B, C, E

2․ Գտնել շրջանագծի շառավիղը և կենտրոնի կոորդինատները, որը տրված է հետևյալ հավասարումով․ ա) x²+y²=9, բ) (x-1)²+(y+2)²=4, գ) (x+3)²+y² =16

ա) Կենտրոն (0,0), R=3
բ) Կենտրոն (1,−2), R=2
գ) Կենտրոն (−3,0), R=4

3․ Գրել 7 շառավղով շրջանագծի հավասարումը, եթե դրա կենտրոնը կոորդինատների սկզբնակետն է:

x2+y2=49

4․ Գրել O (-2; 3) կենտրոնով շրջանագծի հավասարումը, որն անցնում է B(1; 2) կետով:

(x+2)2+(y−3)2=10

5․ Գտնել O(3;1) կենտրոնով և A (6; -3) կետով անցնող շրջանագծի շառավիղը:

R=5

6․ Ինչի՞ է հավասար (x — 11)² + (y + 24)² = 36 հավասարմամբ որոշվող շրջանագծի տրամագիծը:

Տրամագիծ = 12

7. Գրել A(3; — 4) կենտրոնով և R = 7 շառավղով շրջանագծի հավասարումը:

(x−3)2+(y+4)2=49

8․ Գրել AB տրամագծով շրջանագծի հավասարումը, եթե A(2; -1), B(4; 3):

(x−3)²+(y−1)²=5