Թեմա՝ Վեկտորների հասկացությունը։ Վեկտորների հավասարությունը։

Վեկտորը լատիներեն բառ է, որը նշանակում է տանող:

Գծենք որևէ AB  հատված: Նրա մի ծայրակետը, օրինակ՝ A-ն անվանենք սկիզբ (կամ սկզբնակետ), իսկ մյուսը՝ B-ն` վերջ (կամ վերջնակետ): AB հատվածի A-ից B ուղղությունը նշում են սլաքի միջոցով: Արդյունքում ստացվում է ուղղորդված հատված:

Ուղղորդված հատվածը կոչվում է վեկտոր:

Այսպիսով, այն հատվածը, որի համար նշված է, թե նրա ծայրակետերից որն է սկիզբը, իսկ որն է վերջը, կոչվում է ուղղորդված հատված կամ վեկտոր:

Վեկտորները կարելի է նշանակել երկու ձևերով:

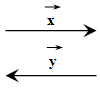
• Երկու մեծատառերի միջոցով, որոնց վրա դրվում է սլաք՝ AB→(կարդում են AB վեկտոր): Առաջին տառը ցույց է տալիս վեկտորի սկիզբը, իսկ երկրորդը՝ վերջը:
• Մեկ փոքրատառով, որի վրա դրվում է սլաք՝ a→  (կարդում են a վեկտոր):

Եթե վեկտորի սկիզբն ու վերջը համընկնում են, ապա այն կոչվում է զրոյական վեկտոր և նշանակվում է՝ 0→:  Հարթության ցանկացած կետ կարելի է համարել զրոյական վեկտոր:

AB հատվածի երկարությունը կոչվում է AB→վեկտորի երկարություն կամ մոդուլ և նշանակվում է՝ ∣AB→∣

∣g→∣=1.5, ∣AB→∣=3 գրառումները նշանակում են, որ g→ վեկտորի երկարությունը հավասար է 1.5 միավորի, իսկ AB→ վեկտորի երկարությունը՝ 3 միավորի:

Զրոյական վեկտորի երկարությունը հավասար է զրոյի՝ ∣0→∣=0

Բազմաթիվ ֆիզիկական մեծություններ, օրինակ՝ ուժը, տեղափոխությունը, արագությունը, բնութագրվում են ոչ միայն թվային արժեքով, այլև տարածության մեջ նրանց ունեցած ուղղությունով:

Մեծությունները, որոնք ունեն թվային արժեք և ուղղություն, կոչվում են վեկտորական մեծություններ:

Մեծությունները, որոնք ունեն միայն թվային արժեք և չունեն ուղղություն, կոչվում են սկալյար մեծություններ:

Սկալյար մեծություններ են, օրինակ՝ երկարությունը, քանակը, խտությունը:

Ոչ զրոյական վեկտորները կոչվում են համագիծ կամ կոլինեար, եթե նրանք գտնվում են կամ նույն ուղղի վրա,  կամ զուգահեռ ուղիղների վրա:

Զրոյական վեկտորը համարվում է համագիծ ցանկացած վեկտորին:

Եթե a→ և b→ վեկտորները համագիծ են, ապա գրում ենք այսպես՝ a→∥b→

Երկու համագիծ վեկտորները կարող են ուղղված լինել կամ միանման, կամ հակառակ:

Առաջին դեպքում վեկտորները կոչվում են համուղղված, իսկ երկրորդ դեպքում՝ հակուղղված:



Համուղղված վեկտորները նշանակում են այսպես՝ a→↑↑b→, իսկ հակուղղվածներն այսպես՝ a→↑↓b→

Զրոյական վեկտորը համարվում է համուղղված ցանկացած վեկտորին:

Հավասար վեկտորներ

Վեկտորները կոչվում են հավասար, եթե նրանք համուղղված են, և նրանց երկարությունները հավասար են:



Եթե a→ և b→ վեկտորները հավասար են, ապա գրում են այսպես՝ a→=b→

Հավասար վեկտորների ուղղությունները համընկնում են, իսկ մոդուլները՝ հավասար են:

Հավասար մոդուլներ ունեցող հակուղղված վեկտորները կոչվում են հակադիր վեկտորներ:



Եթե a→ և b→ վեկտորները հակադիր են, ապա գրում են այսպես՝ a→=−b→

Փոխելով վեկտորի ուղղությունը հակառակով՝ ստանում ենք տրվածին հակադիր վեկտոր՝ AB→=−BA→

Առաջադրանքներ։

1․ Հետևյալ մեծություններից որո՞նք են վեկտորական:

տեղափոխություն

լայնություն

կշիռ

աշխատանք

2․ ABCD ուղղանկյան տրված նկարի օգնությամբ որոշիր AB և BC վեկտորների երկարությունները, եթե հայտնի է, որ AB=10, BC=24

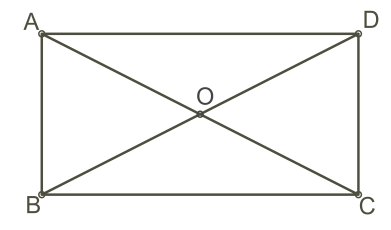
|A^→B∣=10, ∣BC∣=24

AB=10 BC=24։

3․ d→ և z→ վեկտորները հակադիր են: Գտնել z→ վեկտորի երկարությունը, եթե ∣d→∣=15։

z^→=−d^→, ∣d^→∣=15 ∣z^→∣=15

Հուշում՝ Հավասար երկարություն ունեցող հակուղղված վեկտորները կոչվում են հակադիր վեկտորներ:

4․ Ընտրել հակադիր վեկտորները: