Առաջադրանքներ․

1. Գտնել ֆունկցիայի մոնոտոնության միջակայքերը․

Ա)

Մեծանում է՝ (−10, −3) և (0, 5)

Նվազում է՝ (−3, 0) և (5, 10)

Բ)

Նվազում է՝ (−10, 0)

Մեծանում է՝ (0, 10)

Գ)

Ֆունկցիան նվազում է ամբողջ միջակայքում՝
x∈(0, 8)

Դ)

Ֆունկցիան մեծանում է ամբողջ միջակայքում՝

x∈(−8, 0)

Ե)

Մեծանում է՝ (−10, −2) և (2, 10)

Նվազում է՝ (−2, 2)

Զ)

Մեծանում է՝ (−10, −6) և (0, 6)

Նվազում է՝ (−6, 0) և (6, 10)

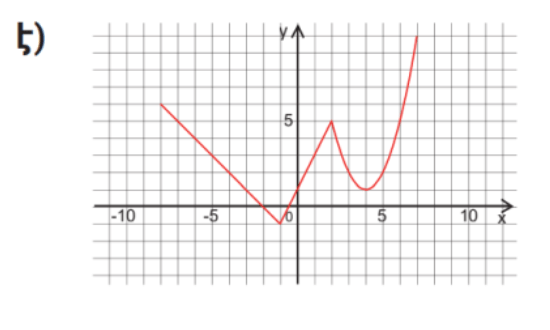
Է)

Նվազում է՝ (−10, −2)

Մեծանում է՝ (−2, 4)

Ը)

Մեծանում է՝ (−10, −6) և (−2, 4)

Նվազում է՝ (−6, −2) և (4, 10)

2․ Գտնել ֆունկցիայի մոնոտոնության միջակայքերը․

ա)

Նվազում է՝ x∈(−6, 0)

Մեծանում է՝ x∈(0, 2)

Կայուն է՝ x∈(2, 4)

բ)

Նվազում է՝ x∈(−6, −2)

Մեծանում է՝ x∈(−2, 2)

Կայուն է՝ x∈(2, 6)

գ)

Մեծանում է՝ x∈(−6, 4)

Նվազում է՝ x∈(4, 6)

դ)

Նվազում է՝ x∈(−6, −2)

Մեծանում է՝ x∈(−2, 4)

Նվազում է՝ x∈(4, 6)

ե)

Մեծանում է՝ x∈(−6, −3)

Նվազում է՝ x∈(−3, 0)

Մեծանում է՝ x∈(0, 2)

Նվազում է՝ x∈(2, 4)

Մեծանում է՝ x∈(4, 6)

զ)

Մեծանում է՝ x∈(−6, −2)

Նվազում է՝ x∈(−2, 2)

Մեծանում է՝ x∈(2, 6)

է)

Մեծանում է՝ x∈(−6, −2)

Կայուն է՝ x∈(−2, 2)

Մեծանում է՝ x∈(2, 6)

ը)

Նվազում է՝ x∈(−6, 0)

Մեծանում է՝ x∈(0, 2)

Նվազում է՝ x∈(2, 6)

3․ Մոնոտո՞ն է առ․ 2-ում ներկայացված ֆունկցիան: Եթե այո, ապա նշել մոնոտոնության բնույթը․

Հնարավոր է, որ ֆունկցիայի որոշման տիրույթն ամբողջությամբ լինի մոնոտոնության միջակայք: Այդպիսի ֆունկցիաներն անվանում են մոնոտոն: Մոնոտոն ֆունկցիաները լինում են աճող, նվազող, չաճող ու չնվազող:

4․ Մոնոտո՞ն է արդյոք ֆունկցիան: Եթե այո, ապա որոշել մոնոտոնության բնույթը.

մոնոտոն է, և ֆունկցիան մեծացող է

5․ Գտնել 5 թվի և նրա հակադիր թվի գումարը։

5+(−5)=0

6․ Գտնել -8 թվի և նրա հակադիր թվի տարբերությունը։

(−8)−8=−16

7․ Գտնել 3 թվի և նրա հակադիր թվի արտադրյալը։

3×(−3)=−9

8․ Գտնել 12 թվի և նրա հակադիր թվի քանորդը։

12:(−12)=−1

9․ Գտնել -14 թվի և նրա հակադիր թվի քանորդը։

(−14):14=−1