Թեմա՝ Ֆունկցիայի մոնոտոնության և նշանապահպանման միջակայքերը, մեծագույն և փոքրագույն արժեքները։

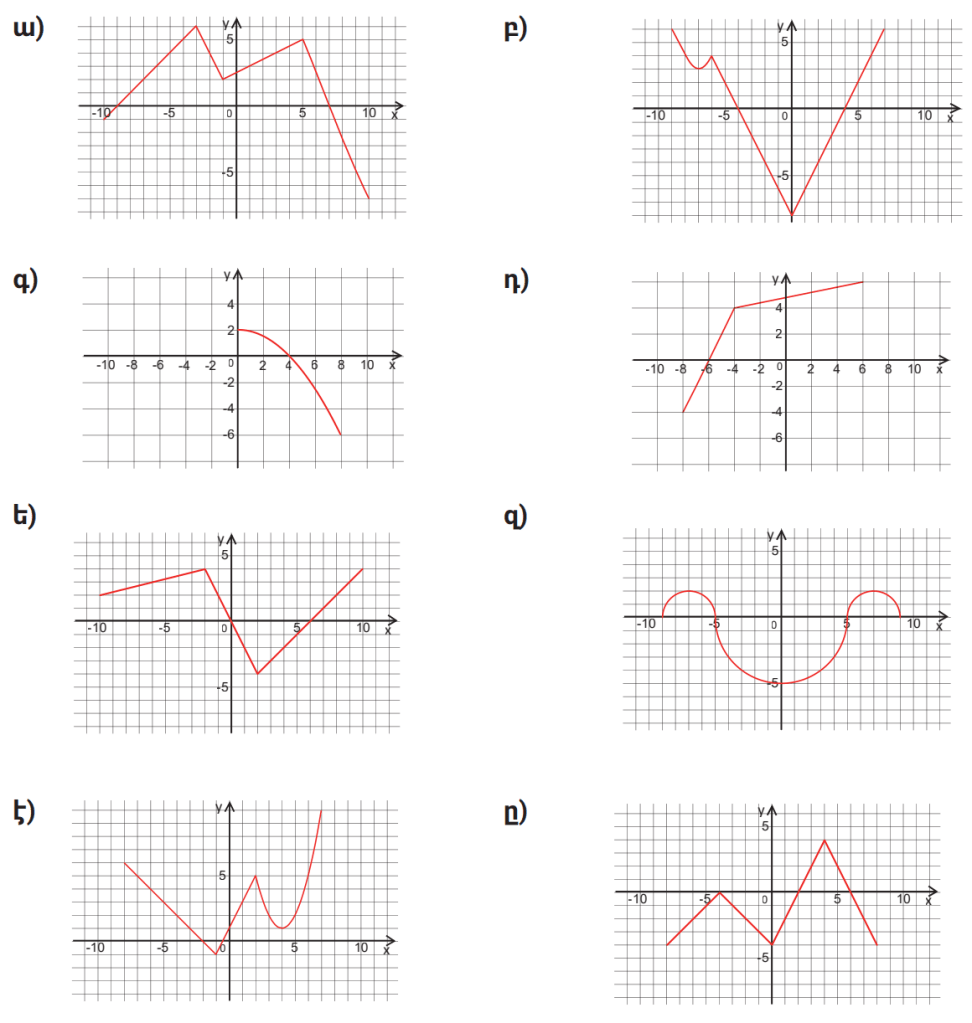
1․ Գտնել ֆունկցիայի մեծագույն և փոքրագույն արժեքները: Ո՞ր կետերում է ընդունում այդ արժեքը։

Ա) մեծագույն 8 (x≈–2), փոքրագույն –8 (x≈9)
Բ) մեծագույն 6 (x≈–9, 9), փոքրագույն –8 (x=0)
Գ) մեծագույն 2 (x≈0), փոքրագույն –6 (x≈8)
Դ) մեծագույն 5 (x≈8), փոքրագույն –3 (x≈–8)
Ե) մեծագույն 5 (x≈–2), փոքրագույն –6 (x≈2)
Զ) մեծագույն 2 (x≈–6, 6), փոքրագույն –5 (x≈0)
Է) մեծագույն 9 (x≈10), փոքրագույն 0 (x≈–2)
Ը) մեծագույն 6 (x≈4), փոքրագույն –6 (x≈0)

2․ Տրված f(x) ֆունկցիայի որոշման տիրույթն է D = [- 5, 5] Հայտնի է, որ f(- 3) = 4 և f(1) = 2 Կարո՞ղ է f(x) ֆունկցիան լինել
ա) աճող
բ) նվազող։

3․ f(x) ֆունկցիայի որոշման տիրույթը (−∞, +∞) միջակայքն է։ Ֆունկցիայի մասին հայտնի է, որ f(0) = 8, f(5) = 8 և f(- 1) = — 2 Կարո՞ղ է արդյոք f(x) ֆունկցիան լինել
ա) նվազող
բ) չնվազող

4․ Տրված f(x) ֆունկցիայի համար հայտնի է, որ այն աճող է [1, 6] միջակայքում և f(1) = 5 f(6) = 11 : Հնարավո՞ր է արդյոք, որ
ա) f(4) = 10 — հնարավոր է
բ) f(4) = 14 — անհնար է չի կարող անցնել 11-ից ավել
գ) f(4) = 5 — անհնար է չի կարող մնալ նույնը, պետք է աճի