Թեմա՝ Պարաբոլի տեղաշարժերը
f(x) = x2 ֆունկցիայի գրաֆիկը աջ/ձախ և վերև/ներքև տեղաշարժելով ու y-ների առանցքների երկայնքով ձգելով՝ կստանանք տարբեր ֆունկցիաների գրաֆիկներ։ Այս դասին ուսումնասիրենք այդ ձևափոխությունները։

1) f(x) = x2 ֆունկցիայի գրաֆիկը 3 միավորով աջ տեղաշարժելով՝ կստանանք f(x−3) = (x−3)2 ֆունկցիայի գրաֆիկը: Այն (3, 0) գագաթով պարաբոլ է ։
y = (x − x 0)2 ֆունկցիայի գրաֆիկը (x0, 0) գագաթով պարաբոլ է։
2) f(x) = (x − x0)2 ֆունկցիայի գրաֆիկը y-ների առանցքի երկայնքով a անգամ ձգելով՝ կստանանք y = a(x − x0)2 ֆունկցիայի գրաֆիկը։
3) f(x) = 2 (x − 3)2 ֆունկցիայի գրաֆիկը 7 միավորով վերև տեղաշարժելով՝ կստանանք f(x) + 7 = 2(x − 3)2 + 7-ի գրաֆիկը։ Այս տեղաշարժիարդյունքում պարաբոլի գագաթը (3, 0) կետից կտեղափոխվի (3, 7) կետը։
Ամփոփենք. y = 2(x − 3)2 + 7 ֆունկցիայի գրաֆիկը y-ների առանցքի երկայնքով 2 անգամ ձգած պարաբոլ է, որի գագաթը (3, 7) կետն է։
y= a(x − x0) 2 + y0 ֆունկցիայի գրաֆիկը y-ների առանցքի երկայնքովa անգամ ձգած և (x0, y0) գագաթով պարաբոլ է։ Եթե a > 0, ապա պարաբոլի ճյուղերն ուղղված են վերև, իսկ a < 0 դեպքում ՝ ներքև: ( x0;y0) կոորդինատներով կետը կոչվում է պարաբոլի գագաթ։
Առաջադրանքներ։
1․ Գծել f(x) = x2 պարաբոլը։ Ո ՞ր ֆունկցիայի գրաֆիկը կստացվի, եթե f(x)-ի գրաֆիկը տեղափոխենք ա) 2 միավորով աջ, բ) 5 միավորով ձախ։
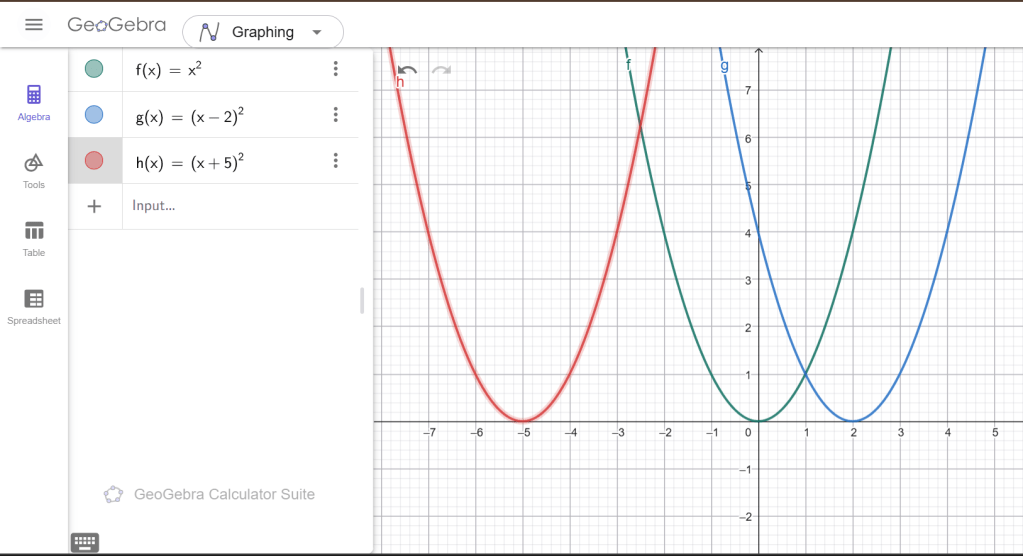
ա) 2 միավորով աջ տեղափոխելիս
y=(x−2)2
բ) 5 միավորով ձախ տեղափոխելիս
y=(x+5)2
2․ Ո ՞ր ֆունկցիայի գրաֆիկը կստացվի, եթե f(x) = 3x2 ֆունկցիայի գրաֆիկը տեղափոխենք ա) 4
միավորով ձախ, բ) 1 միավորով աջ։
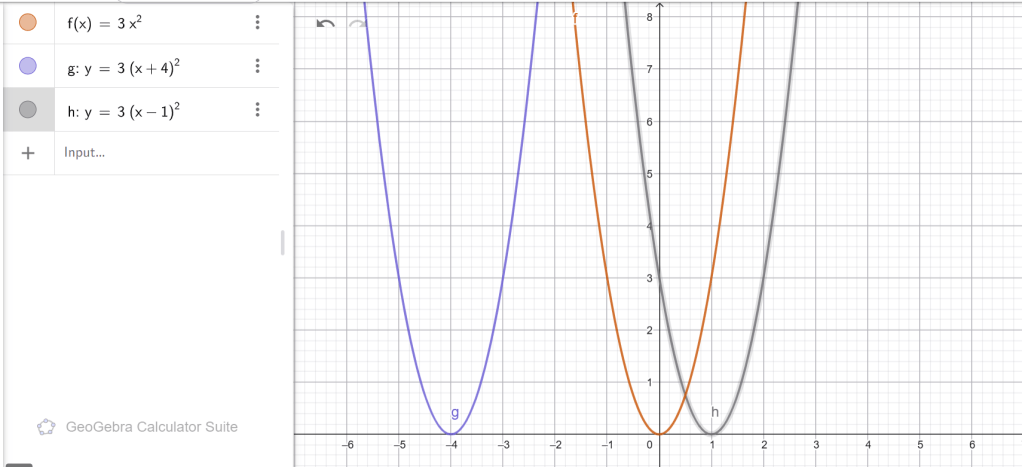
3․ Հայտնի է, որ f(x) ֆունկցիայի գրաֆիկը տեղաշարժելով ա) 5 միավորով աջ, բ) 12 միավորով ձախ՝ ստացվել է y = x2 պարաբոլը։ Գտնել f(x) ֆունկցիայի բանաձևը։
Ա)
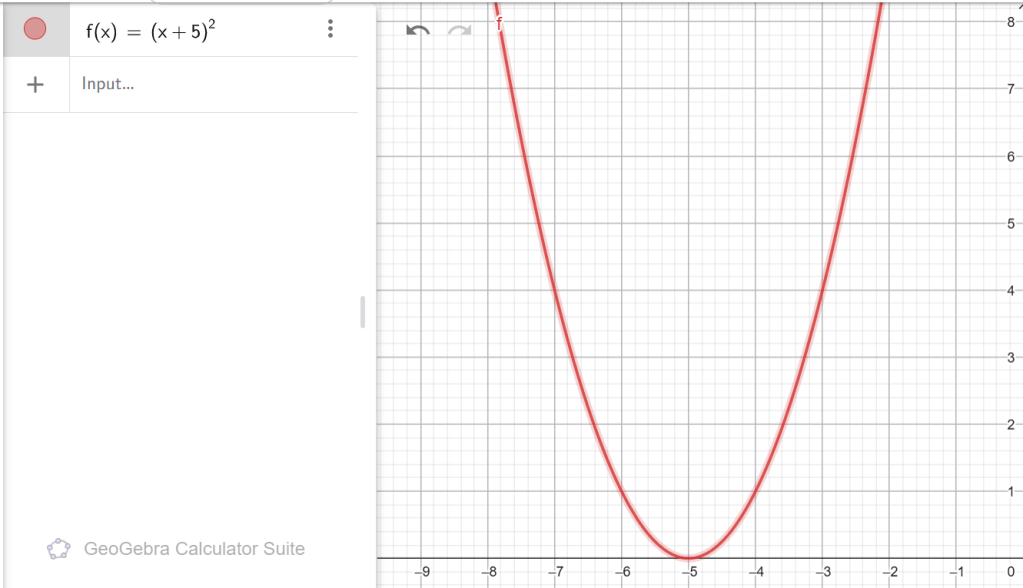
Բ)

4․ Ո ՞ր ֆունկցիայի գրաֆիկը կստացվի, եթե f(x) = x2 պարաբոլը տեղափոխենք.
ա) 2 միավորով աջ և 4 միավորով ներքև,
բ) 5 միավորով ձախ և 1 միավորով վերև,
գ) 2 միավորով ներքև և 1 միավորով աջ,
դ) 3 միավորով ձախ և 5 միավորով ներքև։
Ա)
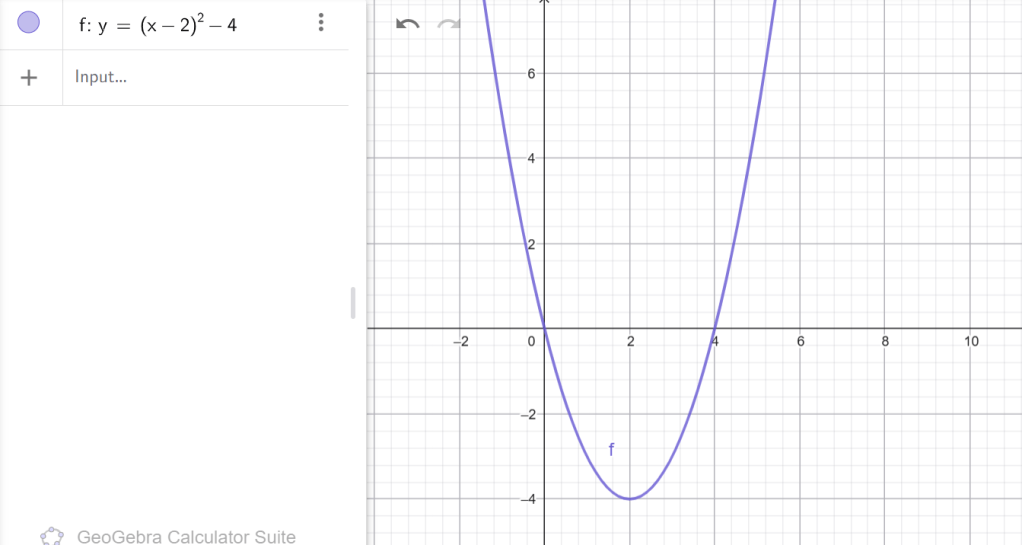
Բ)
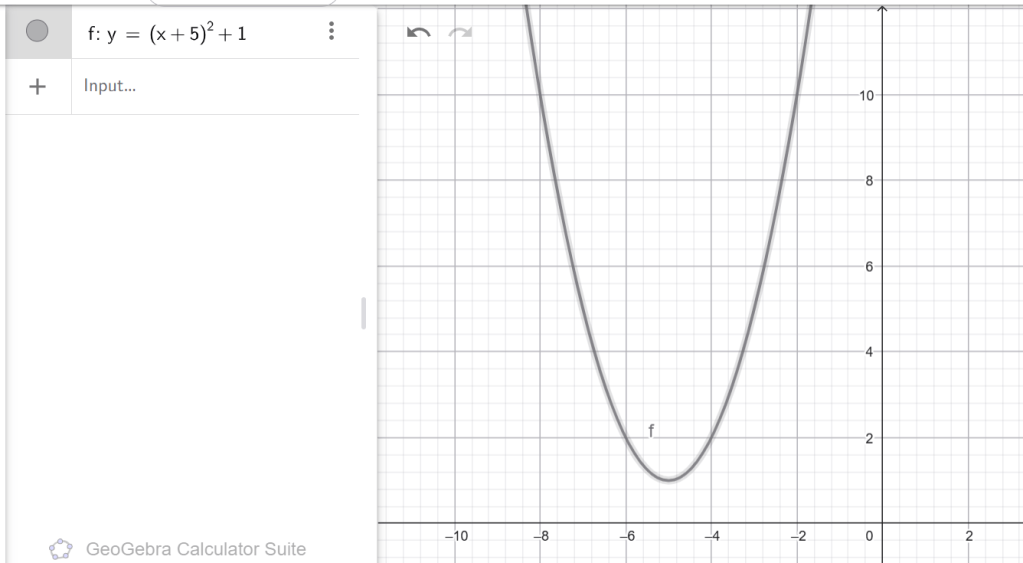
Գ)
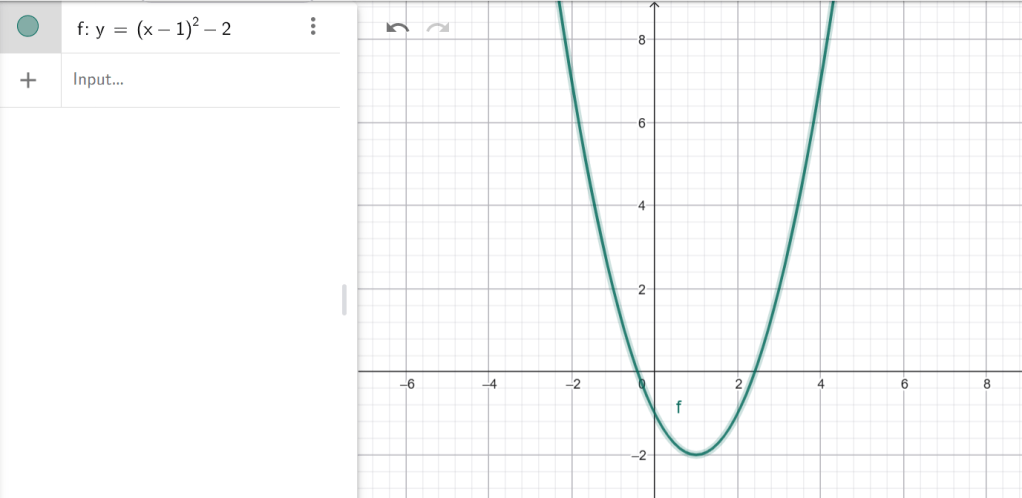
Դ)

5․ Պատկերե՛ք ֆունկցիայի գրաֆիկը.
ա) y = (x + 4) 2, բ) y = (x − 1) 2 − 3, գ) y = (x + 6) 2 + 8, դ) y = (x − 4) 2 + 7։
Ա)
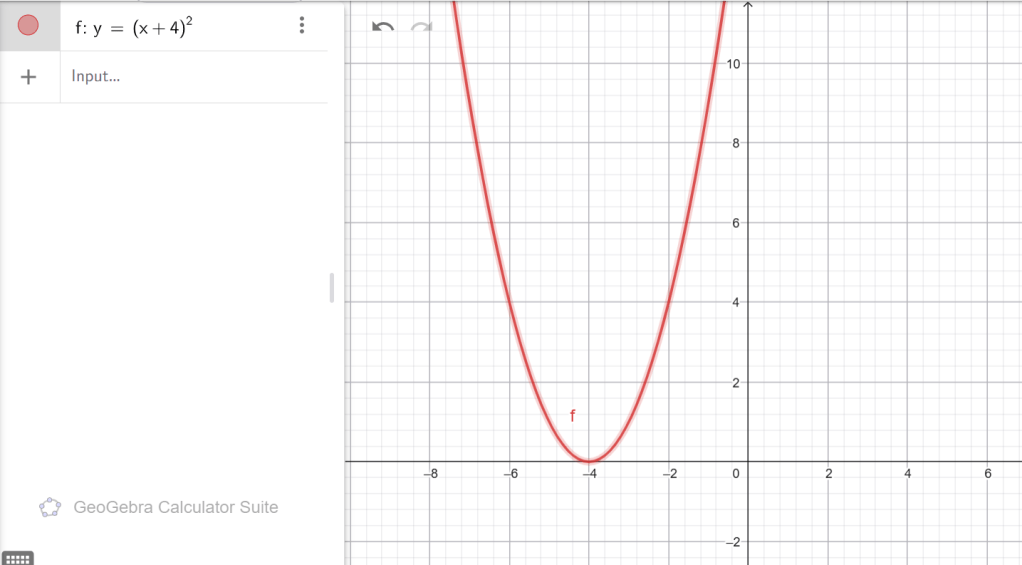
Բ)
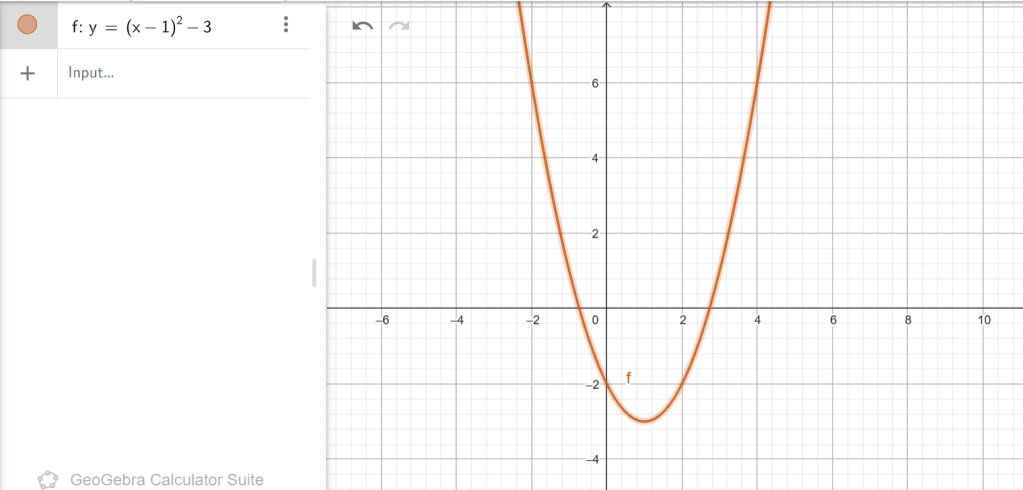
Գ)
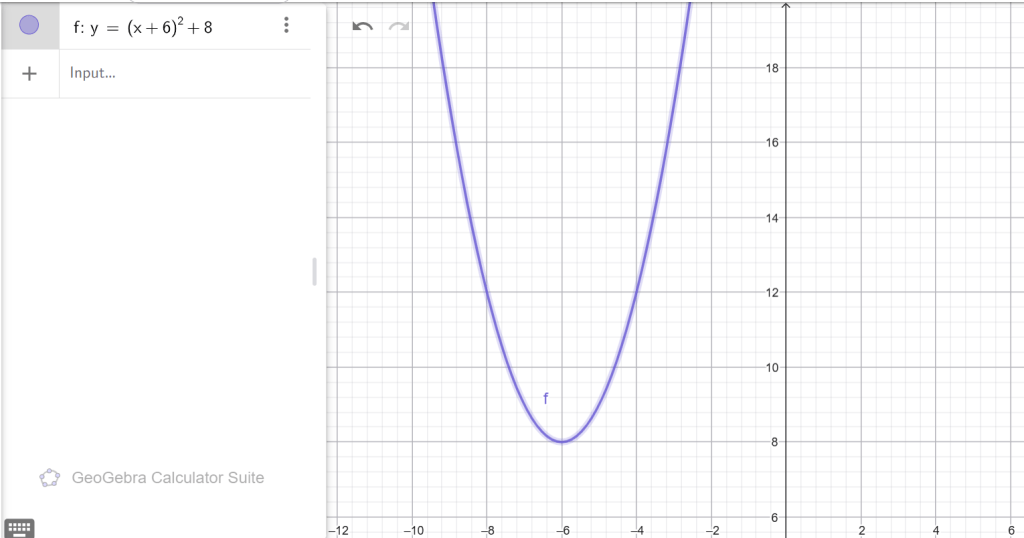
Դ)

6․ Գտնել հետևյալ պարաբոլի գագաթի կոորդինատները.
ա) y = 2(x − 4) 2 , բ) y = x 2 + 5, գ) y = (x + 3)2 + 1, դ) y = 8(x -11)2 - 20։
Ա)
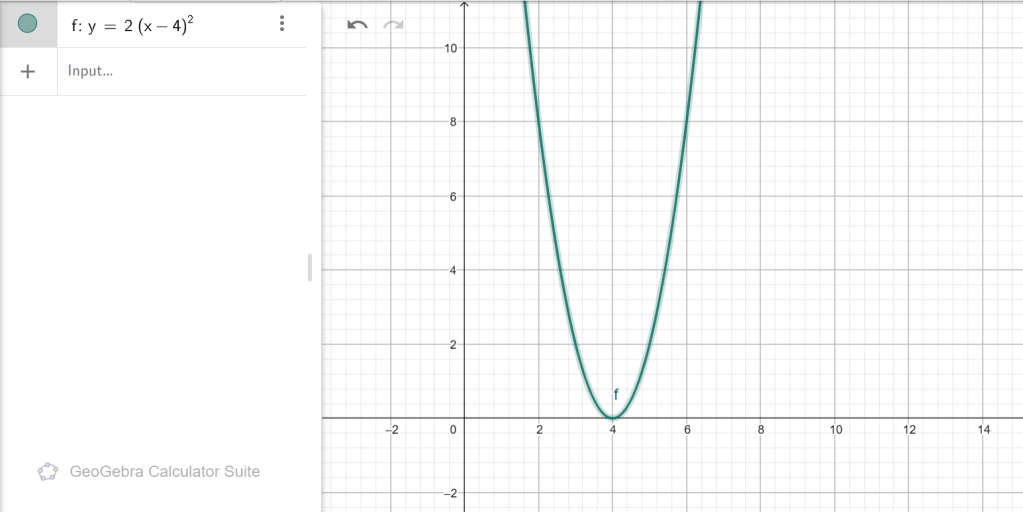
գագաթ՝ (4, 0)
Բ)

գագաթ՝ (0, 5)
Գ)
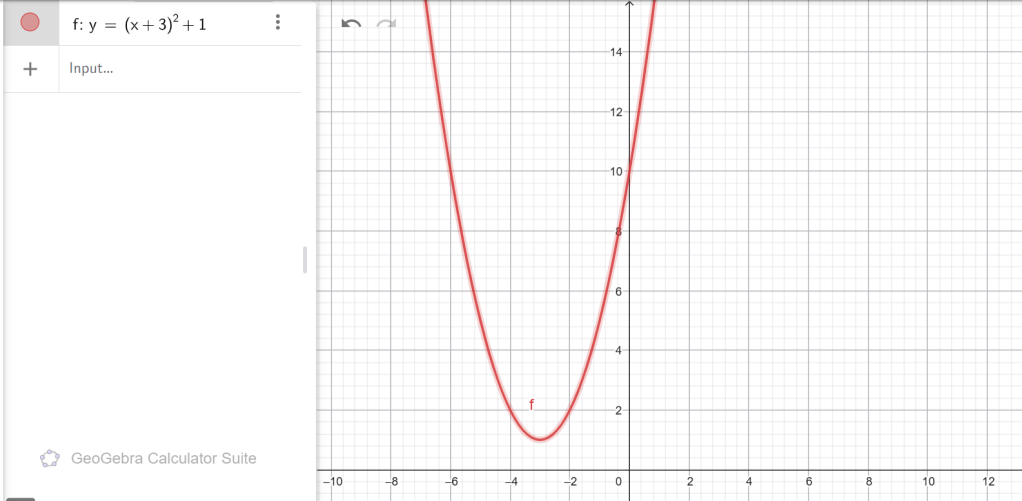
գագաթ՝ (−3, 1)
Դ)
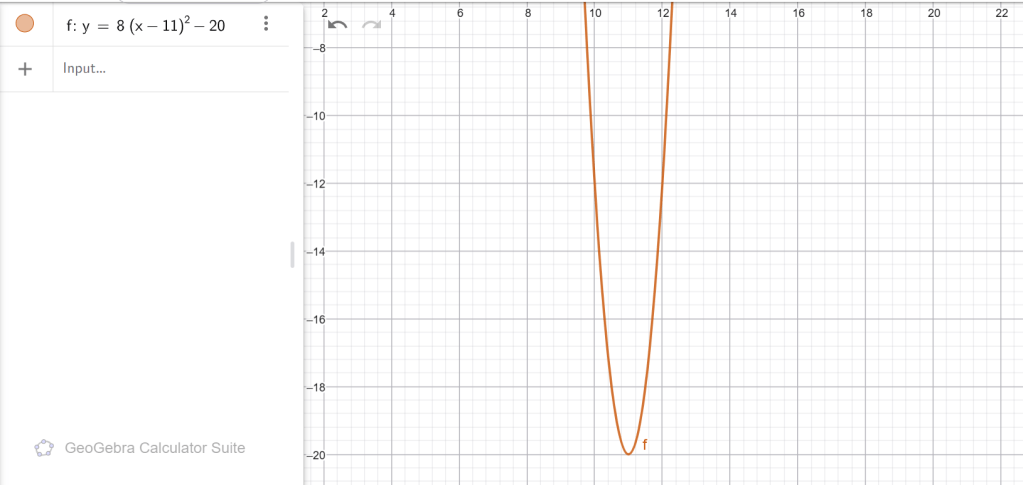
գագաթ՝ (11, −20)
7․ Պարզե՛ք պարաբոլի ճյուղերի ուղղությունը։ Դրանք հատվո՞ւմ են աբսցիսների առանցքի հետ.
ա) y = (x − 1) 2 + 3, բ) y = − 2(x − 5) 2 + 6, գ) y = √5(x + 3)2 − 7,դ) y = − 7(x − 8) 2 − 14, ե) y = 4 x2 − 16, զ) y = − 3(x + 4) 2 − 15:
Ա)
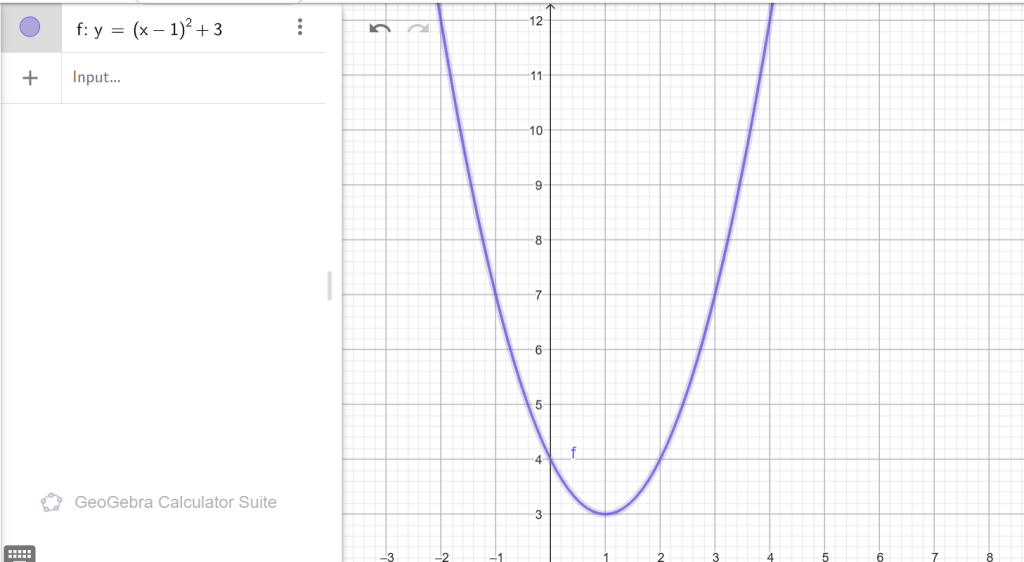
ճյուղերը՝ վերև
OX–ը չի հատում
Բ)
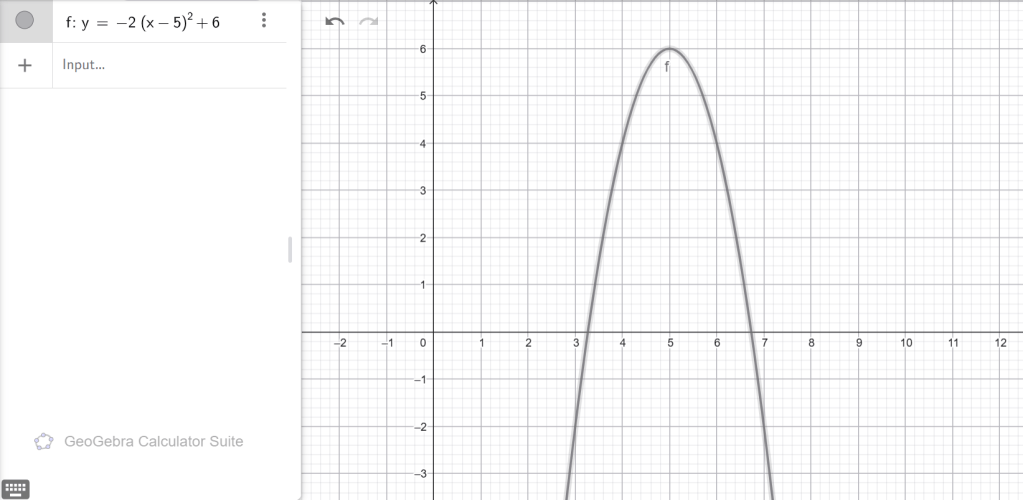
ճյուղերը՝ ներքև
OX–ը հատում է
Գ)
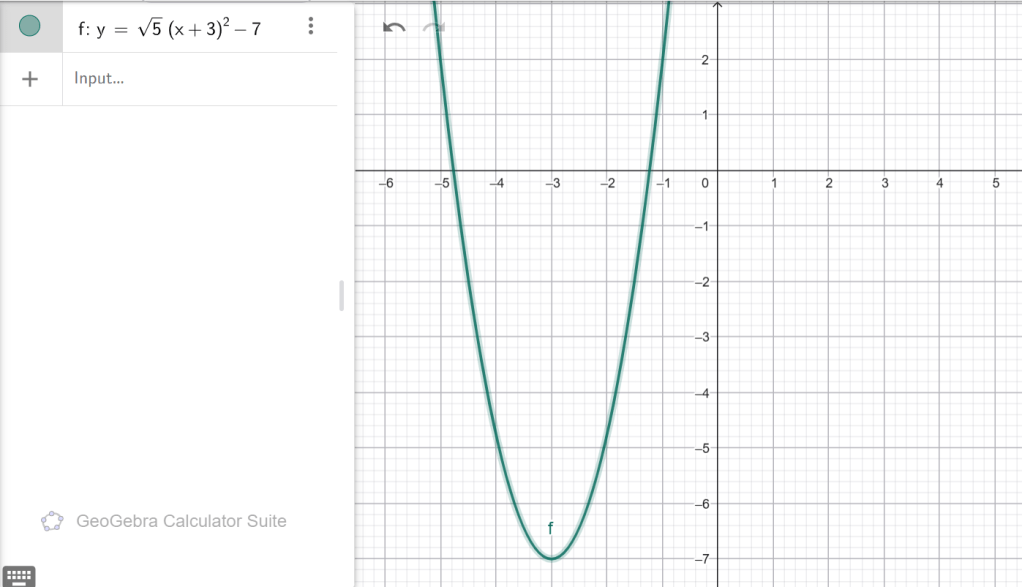
ճյուղերը՝ վերև
OX–ը հատում է
Դ)

ճյուղերը՝ ներքև
OX–ը չի հատում
Ե)
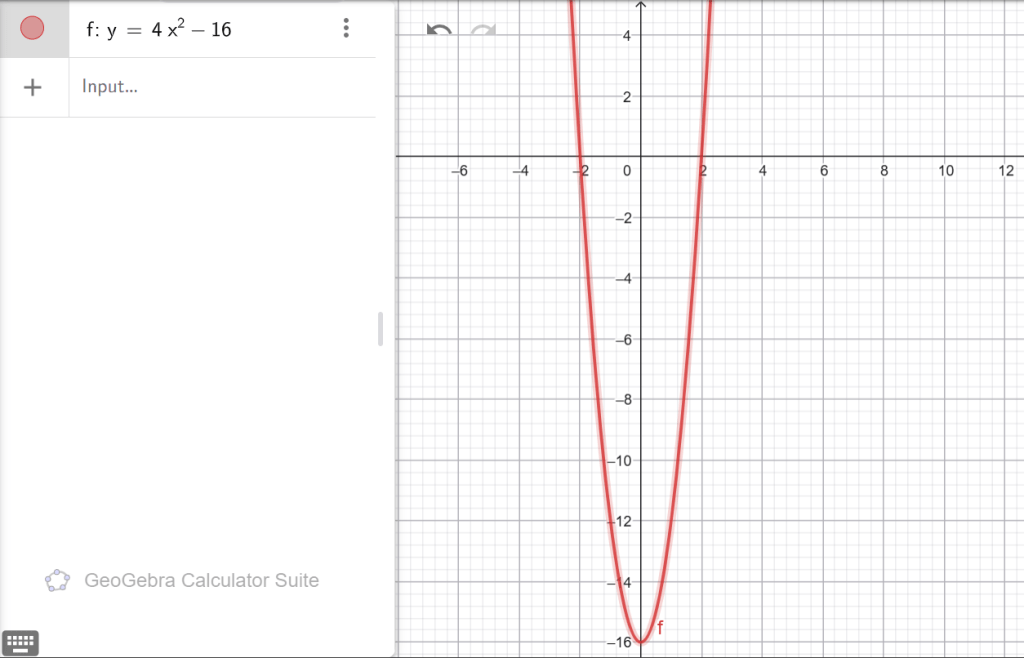
ճյուղերը՝ վերև
OX–ը հատում է
Զ)
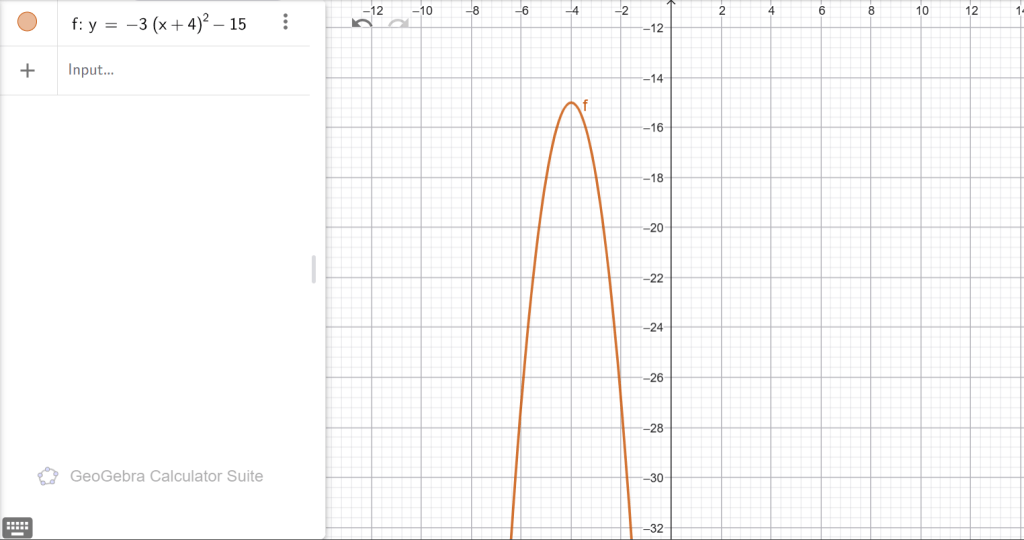
ճյուղերը՝ ներքև
OX–ը չի հատում
