Թեմա՝ Նման եռանկյունների սահմանումը։

Երկու եռանկյուններ կոչվում են նման, եթե նրանց անկյունները համապատասխանաբար հավասար են, և եռանկյուններից մեկի կողմերը համեմատական են մյուսի համապատասխան կողմերին: AB-ն ու A₁B₁-ը, BC-ն ու B₁C₁-ը, AC-ն ու A₁C₁-ը կոչվում են նմանակ կողմեր:

Ուրեմն ABC և A₁B₁C եռանկյունները կոչվում են նման, եթե տեղի ունեն հետևյալ պայմանները.
∠A = ∠A₁, ∠B = ∠B₁, ∠C = ∠C₁,

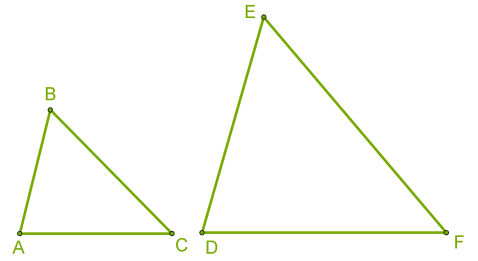
Տրված են ABC և DEF եռանկյունները:

Եթե տրված է, որ AB/DE=BC/EF=AC/DF=k և ∠A=∠D; ∠B=∠E; ∠C=∠F, ապա կարելի է եզրակացնել, որ եռանկյունները նման են:

Այս հանգամանքը գրում ենք այսպես՝ ΔABC∼ΔDEF

Եռանկյունների նմանությունը գրելիս կարևոր է եռանկյունների տառերը գրել ճիշտ հերթականությամբ:

Հավասար անկյուններին համապատասխանում են որոշակի տառեր:

k թիվը, որը հավասար է նման եռանկյունների համապատասխան կողմերի հարաբերությանը, կոչվում է եռանկյունների նմանության գործակից: 

Առաջադրանքներ։

1․ Նմա՞ն են ABC և A₁B₁C₁ եռանկյունները, եթե ∠A = A₁, ∠B = ∠B₁, ∠C=∠C₁, AB = 12 սմ, BC = 8 սմ, AC = 18 սմ, A₁B₁= 6 սմ, B₁C₁ = 4 սմ, A₁C₁ = 9 սմ:

Այո հարաբերություններն՝ 12/6=8/4=18/9=2 Նմանության գործակիցը՝ k=2․

2. ABC և KMN եռանկյունները նման են, ընդ որում՝ AB/MN = BC/NK = AC/MK: ABC և KMN եռանկյունների ո՞ր անկյուններն են համապատասխանաբար հավասար:

Ըստ համապատասխան կողմերի՝ A↔M,  B↔N,  C↔K Դրանով՝ ∠A=∠M,  ∠B=∠N,  ∠C=∠K

3. DC և MN հատվածները երկու նման եռանկյունների կողմերն են, ընդ որում՝ եռանկյուններում դրանց դիմաց ընկած են հավասար անկյուններ:  Գտնել  MN հատվածի երկարությունը, եթե DC=19մ և DC/MN=4/13

Դրված է DC=19 մ և DC/MN=4/13 Ուստի MN=19⋅13/4=247/4=61.75 մ.

4․ ABC և LNM եռանկյունները նման են k=9 նմանության գործակցով: BC և NM հատվածներն այդ եռանկյունների կողմերն են, որոնց դիմաց՝ եռանկյուններում գտնվում են հավասար անկյուններ: Գտնել BC կողմի երկարությունը, եթե NM=10մմ:

k=9 և BC համապատասխանում է NM-ին, NM=10 մմ, ապա BC=9⋅10=90 մմ.

5․ BCA և MKL եռանկյունները նման են, ընդ որում BC, MK և CA, KL կողմերը զույգ առ զույգ համեմատական են: Հաշվել  MK կողմի երկարությունը, եթե BC=2սմ, CA=18սմ և KL=54սմ:

Տրված է՝ եռանկյունները նման են, BC=2 սմ, CA=18 սմ, KL=54 սմ։
Քանի որ CAև KL կողմերը համապատասխան են, ապա BC/MK=CA/KL⇒MK=BC⋅KL/CA=2⋅54/18=6 սմ.

Պատասխան՝ MK=6