Հարցեր և խնդիրներ
198.ABC եռանկյունում AC = sqrt(2) սմ, BC = 1 սմ, ∠ABC = 45°: Գտե՛ք BAC անկյունը:
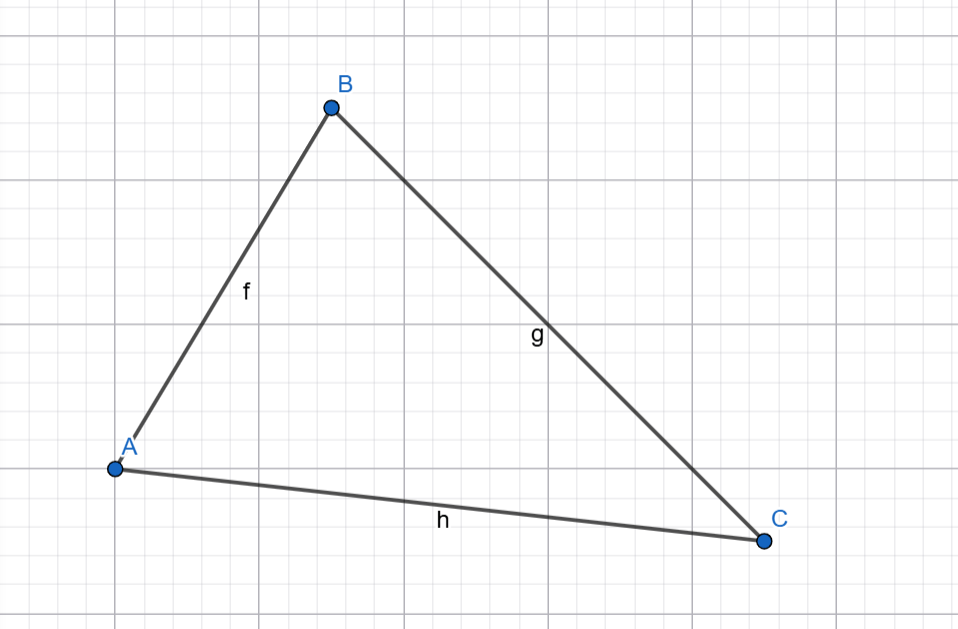
sin∠BAC=1|2 ∠BAC=30∘
199.Եռանկյան կողմը 12 սմ է, իսկ դրա դիմացի անկյունը` 45°։ Գտեք այդ եռանկյանն արտագծած շրջանագծի շառավիղը:
R = a|2sinA = 2⋅sin45°12 =6√2 սմ
200.Եռանկյանն արտագծած շրջանագծի շառավիղը 5 դմ է, անկյուններից մեկը՝ 60°: Գտե՛ք այդ անկյան դիմացի կողմը:
a=A|2Rsin= 2⋅5⋅sin60°=5√3 դմ
201.Եռանկյանն արտագծած շրջանագծի շառավիղը հավասար է կող– մերից մեկին: Գտե՛ք այդ կողմի դիմացի անկյունը:
R=a|2sinA sin A=21 A=30°
202.Ապացուցեք, որ 120° անկյունով հավասարասրուն եռանկյանն արտագծած շրջանագծի շառավիղը հավասար է սրունքին:
R=a|2sin120°=a|2⋅2√3=a|√3≈a
203.Օգտվելով սինուսների թեորեմից՝ լուծեք 164 խնդիրը:
164.Գտեք AC = 10 սմ հիմքով և BC = 13 սմ սրունքով ABC եռանկյանն արտագծած շրջանագծի շառավիղը:
cosB=132+132-102|2⋅13⋅13=119|169 sinB=120|169
204.Ապացուցեք, որ նման եռանկյուններին արտագծած շրջանագծերի շառավիղների հարաբերությունը հավասար է նմանության գործակցին:
Նման եռանկյունների կողմերի հարաբերությունը՝ .
Շառավիղը r=pS, որտեղ S՝ տարածք, p՝ պերիմետր:
Նման եռանկյունների տարածքների հարաբերությունը S1/S2=k2, պերիմետրերի հարաբերությունը p1/p2=k:
r1/r2=S1/p1|S2/p2=k2|k= k
r1:r2=k
205.Հավասարասրուն եռանկյան հիմքը 12√3 սմ է, հիմքին առընթեր անկյունը 60° է: Գտե՛ք այդ եռանկյանն արտագծած շրջանագծի շառավիղը:
Հիմքից բարձրությունը h=BC|2⋅tan60°=6√3⋅3=1√8
Տարածք S=1|2 ⋅ BC ⋅ h=21⋅12√3⋅18=108√3
Պերիմետր p=(AB+AC+BC)/2. Հավասարաչափ մոտեցմամբ AB=AC=12 p=(12+12+123)/2 ≈ 22.39
Շառավիղ r=S/p=6 սմ
r=6 սմ
206.R շառավղով շրջանագծի A կետից տարված են AB և AC լարերը: Գտե՛ք ABC եռանկյան անկյունները, եթե AC = √2 x R AB = R :
AB=R sinC=1/2 C=30°
AC=√2R sinB=√2/2 B=45°
A=180°−B−C=180°−45°−30°=105°
∠A=105°,∠B=45°,∠C=30°
